History and applications

Logarithmic plots

Suppose that you have a set of data points \((x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\) from an experiment or some observations, and you see that \(y\) grows or decays with respect to \(x\). You wish to find out whether the growth or decay is exponential, or obeys a power law, or otherwise. A useful way to determine an exponential or power-law relationship is by using logarithmic plots.

For instance, if \(y\) is exponentially related to \(x\), that is, if \(y = C e^{kx}\) for some constants \(C\) and \(k\), then

\[ \log_e y = kx + \log_e C, \]

so the graph of \(\log_e y\) against \(x\) will be a straight line whose gradient is the continuous growth/decay rate \(k\). Similarly, if \(y\) is related to \(x\) by a power law, \(y = C x^{\alpha}\), then

\[ \log_e y = \alpha \log_e x + \log_e C, \]

so the graph of \(\log_e y\) against \(\log_e x\) will be a straight line of gradient \(\alpha\).

We consider, as an example, some data taken from a 1905 experiment on radioactive decay (see the References section). The physicists Meyer and von Schweidler took measurements of radioactive activity \(A\) from a substance at various times \(t\), measured in days. (The unit for radioactive activity is not of interest here.)

Measurements of radioactivity

\(t\) (time in days)	\(A\) (activity)
0.2	35.0
2.2	25.0
4.0	22.1
5.0	17.9
6.0	16.8
8.0	13.7
11.0	12.4
12.0	10.3
15.0	7.5
18.0	4.9
26.0	4.0
33.0	2.4
39.0	1.4
45.0	1.1

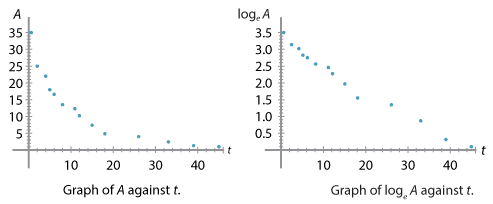
We can plot the graph of \(A\) against \(t\) and the graph of \(\log_e A\) against \(t\), as follows.

Detailed description

We see that the graph of \(A\) against \(t\) looks rather close to exponential decay, although with a few bumps, and the graph of \(\log_e A\) against \(t\) is quite close to linear, again with some bumps. These bumps might indicate some contamination, experimental error, or multiple types of radioactive substance in the sample. In practice, establishing simple mathematical relationships from empirical data can be difficult. However, exponential decay of radioactive substances is by now a well-established scientific fact.

Next page - Appendix - Solving a differential equation using an equilibrium value