Content

Radioactive decay and half-life

Decay of carbon-14

Carbon-14 is a radioactive isotope of carbon, containing 6 protons and 8 neutrons, that is present in the earth's atmosphere in extremely low concentrations.2

It is naturally produced in the atmosphere by cosmic rays (and also artificially by nuclear weapons), and continually decays via nuclear processes into stable nitrogen atoms.

Suppose we have a sample of a substance containing some carbon-14. Let \(m\) be the mass of carbon-14 in nanograms after \(t\) years. 3

It turns out that, if the sample is isolated, then \(m\) and \(t\) approximately 4 satisfy the differential equation

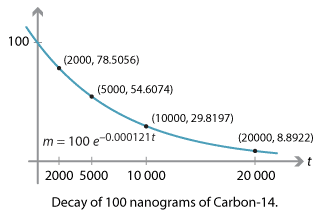
\[\dfrac{dm}{dt} = -0.000121 \, m.\]

Suppose our sample initially contains 100 nanograms of carbon-14. Let's investigate what happens to the sample over time.

First, we can solve the differential equation. Since \(m\) has a continuous decay rate of \(-0.000121\), a general solution to the differential equation is

\[ m(t) = C e^{-0.000121 \, t}, \]

where \(C\) is a constant. Substituting the initial condition \(t = 0\), \(m = 100\) gives \(C = 100\), so

\[ m(t) = 100 \, e^{-0.000121 \, t}. \]

With this formula, we can calculate the amount \(m\) of carbon-14 over the years.

Mass of carbon-14 in sample
\(t\) (years) \(m\) (ng to 4 decimal places)
0 100.0000
100 98.7973
1000 88.6034
2000 78.5056
5000 54.6074
\(10\ 000\) 29.8197
\(20\ 000\) 8.8922

Every year, the mass \(m\) of carbon-14 is multiplied by \(e^{-0.000121} \approx 0.999879\). After 100 years, 98.7973 nanograms still remain. After 1000 years, we still have 88.6034 nanograms. But after 5000 years, however, almost half of the carbon-14 has decayed.

Graph showing the decay of 100 nanograms of Carbon-14.
Detailed description

Half-life of carbon-14

Example

How long does it take for precisely half of the carbon-14 in the sample to decay; that is, when does \(m=50\)? Give the answer to three significant figures.

Solution

The mass of carbon-14 in our sample is given by

\[ m(t) = 100 \, e^{-0.000121 \, t}. \]

So we solve \(50 = 100 \, e^{-0.000121 \, t}\), which gives \(e^{-0.000121 \, t} = \dfrac{1}{2}\). Hence,

\[ t = \dfrac{\log_e \dfrac{1}{2}}{-0.000121} \approx 5730 \text{ years (to three significant figures).} \]

The time period calculated in this example is called the half-life of carbon-14. In fact over any period of 5730 years, the amount of carbon-14 in an isolated sample will decay by half. This fact is used in radiocarbon dating to determine the age of fossils up to \(60\ 000\) years old. Roughly speaking, while an organism is alive, its interactions with its environment maintain a constant ratio of carbon-14 to carbon-12 in the organism; but after it dies, the carbon-14 is no longer replenished, and the ratio of carbon-14 to carbon-12 decays in a predictable way. (See Wikipedia Open new window for more on radiocarbon dating.)

Exercise 1

Explain why the mass of carbon-14 in the sample is given (approximately) by

\[ m(t) = 100 \, \Bigl( \dfrac{1}{2} \Bigr)^{\tfrac{t}{5730}}, \]

and hence explain why the amount of carbon-14 in the sample decays by half over any period of 5730 years.

Half-life in general

In general, whenever a quantity \(x(t)\) obeys an exponential decay equation

\[ x(t) = C e^{kt}, \]

where the continuous decay rate \(k\) is negative, then the quantity \(x\) has a half-life \(T\). After any time period of length \(T\), the quantity \(x\) decreases by half. Let us see why.

As \(k\) is negative, the factor \(e^{kt}\) decreases from 1 (at \(t=0\)) towards 0 (as \(t\) approaches \(\infty\)). Therefore there is a time \(t=T\) such that

\[ e^{kT} = \dfrac{1}{2}. \]

We now solve for \(T\) and obtain

\begin{align*} kT &= \log_e \dfrac{1}{2} \\ &= - \log_e 2, \end{align*} so \[ T = - \dfrac{1}{k} \log_e 2. \]

This \(T\) is the half-life. From time \(t=0\) to time \(t=T\), the factor \(e^{kt}\) decreases from \(e^0 = 1\) to \(e^{kT} = \dfrac{1}{2}\), that is, decreases by half. Similarly, over any time period of length \(T\), the term \(e^{kt}\) decreases by half. 5

Note that, when \(k = -0.000121\), we obtain \(T = 5730\), in agreement with our calculation for carbon-14.

Next page - Content - Population growth and doubling time