Content
A differential equation for exponential growth and decay
Consider the equation
\[\dfrac{dx}{dt} = kx,\]where \(t\) and \(x\) are variables and \(k\) is a constant with \(k \neq 0\). As an equation involving derivatives, this is an example of a differential equation. We often think of \(t\) as measuring time, and \(x\) as measuring some positive quantity over time. That is, \(x\) is a function of time.
The number \(k\) is called the continuous growth rate if it is positive, or the continuous decay rate if it is negative.1
There are many quantities in the real world that approximately obey an equation similar to this one, as we will see shortly. We will first solve the equation in general.
Taking the reciprocal of both sides and noting (via the chain rule) that \(\dfrac{dx}{dt} \cdot \dfrac{dt}{dx} = 1\) gives
\[ \dfrac{dt}{dx} = \dfrac{1}{kx}. \]To solve this equation, we integrate \(\dfrac{1}{kx}\). Recall that \(k\) is a constant and we are assuming that \(x\) is positive. So we obtain
\begin{align*} t &= \int \dfrac{1}{kx} \, dx \\ &= \dfrac{1}{k} \int \dfrac{1}{x} \, dx \\ &= \dfrac{1}{k} \log_e x + c, \end{align*}where \(c\) is a constant of integration.
Rearranging this equation to express \(x\) in terms of \(t\), we have
\[ x = e^{k(t-c)}. \]We can simplify by noting (using index laws) that
\[ e^{k(t-c)} = e^{kt-kc} = e^{-kc} \, e^{kt} \]and the first factor \(e^{-kc}\) is just a positive constant, which we call \(C\). The general solution to the differential equation is then
\[ x(t) = C e^{kt}, \]where \(C\) is any positive constant. It's easy to verify that any such function is a solution: differentiating \(x = C e^{kt}\) with respect to \(t\) gives \(k\) times \(x\).
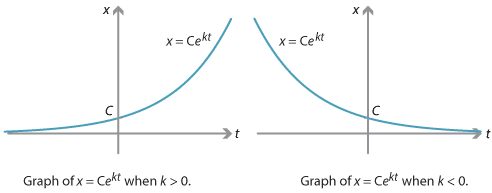
Depending on whether \(k\) is positive or negative, the quantity \(x\) grows or decays with respect to \(t\), as shown in the following graphs.
Note. If we do not assume that \(x\) is positive, then the general solution to the differential equation \(\dfrac{dx}{dt} = kx\) is given by \(x(t) = C e^{kt}\), where \(C\) is any real constant.We have found that the differential equation \(\dfrac{dx}{dt} = kx\) has infinitely many solutions; any value of \(C\) gives a solution. If we have more information, such as the initial value of \(x\), then the value of \(C\) can be determined.
Example
- Find all solutions to the differential equation \[ \dfrac{dp}{dt} = 3p. \]
- Find all solutions to this differential equation if we know that \(p=7\) when \(t=0\).
- The variable \(p\) plays the role of \(x\) in the preceding discussion. With continuous growth rate \(k=3\), the general solution is \[ p(t) = C e^{3t}, \] where \(C\) is any real constant. This is a solution for any real \(C\).
- Since \(p(0)=7\), we obtain \(C=7\), so there is a unique solution \(p(t) = 7 e^{3t}\).
Since derivatives measure rates of change, a differential equation tells us about how one variable changes with respect to another. In general, different starting values for the variables lead to different solutions. Thus, when we use differential equations to model situations in the real world, we often also have initial conditions for the variables, which determine a unique solution.