Answers to exercises

Exercise 1

We can form a gradient diagram for this function.

Value of \(x\) 1 3
Sign of \(f'(x)\) − 0 − 0 +
Slope of graph \(y=f(x)\) \(\diagdown\) — \(\diagdown\) — \(\diagup\)

There is a stationary point of inflexion at \(x=1\), and a local minimum at \(x=3\).

Exercise 2
Let \(f(x) = x^3-5x^2+3x+2\). The derivative is \(f'(x) = 3x^2-10x+3 = (3x-1)(x-3)\). So the stationary points are \(x=\dfrac{1}{3}\) and \(x=3\). Hence, there is a local maximum at \(x=\dfrac{1}{3}\), and a local minimum at \(x=3\).
Exercise 3
The inflexion points are \(x=0\) and \(x=-14\).
Exercise 4
We are given \(f'(x) = x^3(x^2-5) = x^5 -5x^3\). So the stationary points are \(x=0\), \(x=\sqrt{5}\) and \(x= -\sqrt{5}\). The second derivative is \(f''(x) = 5x^4-15x^2 = 5x^2(x^2 - 3)\).
Exercise 5

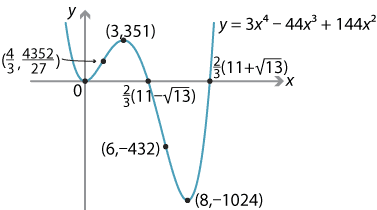
Let \(y = 3x^4-44x^3+ 144x^2\). Then the first and second derivatives are

\begin{align*} \dfrac{dy}{dx} &= 12x^3-132x^2+288x = 12x(x^2-11x+24) = 12x(x-3)(x-8) \\ \dfrac{d^2y}{dx^2} &= 36x^2-264x+288 = 12(3x^2-22x+24) = 12(3x-4)(x-6). \end{align*}
  1. We first find the \(x\)-intercepts: \begin{align*} 3x^4-44x^3+144x^2 &= 0 \\ x^2(3x^2-44x+144) &= 0, \end{align*} which gives \(x=0\) or \(x=\dfrac{2}{3}(11-\sqrt{13})\) or \(x=\dfrac{2}{3}(11+\sqrt{13})\).
  2. We have \(\dfrac{dy}{dx}=12x(x-3)(x-8)\). So \(\dfrac{dy}{dx}=0\) implies \(x=0\) or \(x=3\) or \(x=8\).
  3. Value of \(x\) 0 3 8
    Sign of \(\dfrac{dy}{dx}\) − 0 + 0 − 0 +
    Slope of graph \(\diagdown\) — \(\diagup\) — \(\diagdown\) — \(\diagup\)
  4. We use the second derivative test:
    • at \(x=0\), we have \(\dfrac{d^2y}{dx^2} = 288 > 0\), so there is a local minimum
    • at \(x=3\), we have \(\dfrac{d^2y}{dx^2} = -180 < 0\), so there is a local maximum
    • at \(x=8\), we have \(\dfrac{d^2y}{dx^2} = 480 > 0\), so there is a local minimum.
  5. As \(x \to \infty\), \(y \to \infty\), and as \(x \to -\infty\), \(y \to \infty\).
  6. \(\dfrac{d^2y}{dx^2} =0\) implies \(x = \dfrac{4}{3}\) or \(x=6\). The second derivative changes from positive to negative at \(x=\dfrac{4}{3}\), and from negative to positive at \(x=6\). So there are points of inflexion at \(x=\dfrac{4}{3}\) and \(x=6\).

Graph of y = 3x to the power 4 minus 44 x cubed plus 144 x squared.

Exercise 6
Let \(y=4x^3-18x^2+48x-290\). The first and second derivatives are \begin{align*} \dfrac{dy}{dx} &= 12x^2-36x+48 = 12(x^2-3x+4) \\ \dfrac{d^2y}{dx^2} &= 12(2x-3). \end{align*}
  1. The \(y\)-intercept is \(y=-290\). We now find the \(x\)-intercepts: \begin{align*} 4x^3-18x^2+48x-290 &= 0 \\ 2x^3-9x^2+24x-145 &= 0 \\ (x-5)(2x^2+x+29) &= 0. \end{align*} The quadratic has no real solutions, and so the only \(x\)-intercept is \(x=5\).
  2. \(\dfrac{dy}{dx} = 12(x^2-3x+4)\). The discriminant is \(12(9-16)<0\). Hence, \(\dfrac{dy}{dx}>0\), for all \(x\), and there are no stationary points.
  3. The function is increasing, for all \(x\).
  4. There are no local maxima or minima.
  5. As \(x \to \infty\), \(y \to \infty\), and as \(x \to -\infty\), \(y \to -\infty\).
  6. \(\dfrac{d^2y}{dx^2} = 12(2x-3)\). The second derivative changes from negative to positive at \(x=\dfrac{3}{2}\). So there is a point of inflexion at \(x=\dfrac{3}{2}\).

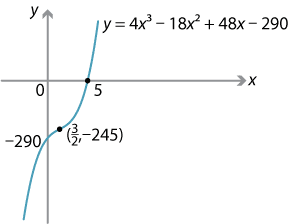
Graph showing point of inflexion.

Exercise 7
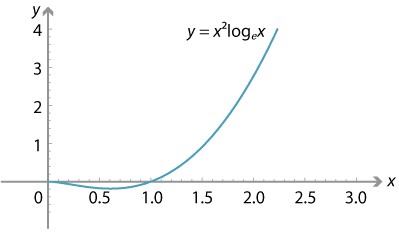
Define \(f \colon (0,\infty) \to \mathbb{R}\) by \(f(x) = x^2\log_e x\). Then \begin{align*} f'(x) &= 2x\log_e x + x^2 \times \dfrac{1}{x} = 2x\log_e x + x = x(2\log_e x + 1) \\ f''(x) &= 2\log_e x + 2 + 1 = 2\log_e x + 3. \end{align*}
  1. For \(x > 0\), we have \(f(x) = 0 \iff \log_e x = 0 \iff x = 1\). So the \(x\)-intercept is 1.
  2. We have \(f'(x) = x(2\log_e x + 1)\). So \(f'(x) = 0\) implies \(x = e^{-\frac{1}{2}}\). There is a stationary point at \(x = e^{-\frac{1}{2}}\).
  3. We have \[ f'(x) > 0 \ \iff\ x(2\log_e x + 1) > 0 \ \iff\ 2\log_e x + 1 > 0 \ \iff\ x > e^{-\frac{1}{2}}, \] and so \(f'(x) < 0 \iff 0 < x < e^{-\frac{1}{2}}\).
  4. \(f''(e^{-\frac{1}{2}}) = 2 > 0\). Hence, there is a local minimum at \(x = e^{-\frac{1}{2}}\).
  5. As \(x \to \infty\), \(f(x) \to \infty\).
  6. We have \(f''(x) = 2\log_e x + 3\). So \[ f''(x) > 0 \ \iff\ x > e^{-\frac{3}{2}}, \qquad f''(x) < 0 \ \iff\ 0 < x < e^{-\frac{3}{2}}. \] There is a point of inflexion at \(x=e^{-\frac{3}{2}}\).

Graph of y = x squared log base e of x.

A second graph is drawn here to highlight the important points.

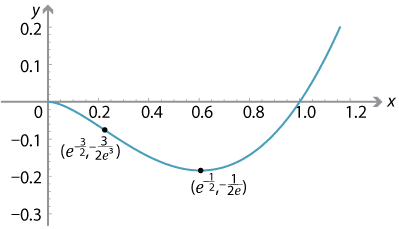
Graph of y = x squared log base e of x from x = 0 to x =1.2.

Exercise 8
Define \(f \colon [-1,2] \to \mathbb{R}\) by \(f(x) = x^2(x+4)\). The first and second derivatives are \[ f'(x) = 3x^2+8x,\qquad f''(x) = 6x+8. \] So \(f'(x) = 0\) when \(x=0\) or \(x=-\dfrac{8}{3}\). The second value is outside the required domain. Since \(f''(0) = 8 > 0\), there is a local minimum at \(x=0\), with \(f(0) = 0\). We now find the value of the function at the endpoints: \(f(-1) = 3\) and \(f(2) = 24\).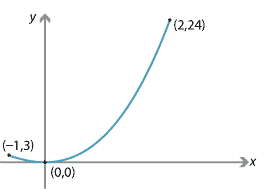

Graph of y = x squared (x plus 4) from x = minus 1 to 2.

The minimum value of the function is 0 and the maximum value is 24.

Exercise 9

Let \(x\) km, \(x\) km and \(y\) km be the lengths of fencing of the three sides of the rectangle to be enclosed. Then \(y = 8 - 2x\).

Let \(A(x)\) km\(^2\) be the area of the enclosed land. Then \(A(x) = x(8-2x) = 8x-2x^2\). The first two derivatives are

\[ A'(x) = 8 -4x \qquad\text{and}\qquad A''(x) = -4. \]

So \(A'(x) = 0\) implies \(x = 2\). Since \(A''(2) = -4 < 0\), there is a local maximum at \(x = 2\). The rectangle of maximum area has dimensions 2 km \(\times\) 4 km, and the maximum area is 8 km\(^2\).

Exercise 10
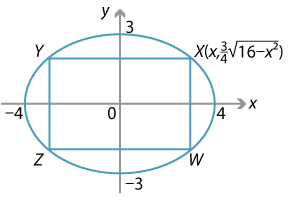
  1. The ellipse has equation \(\dfrac{x^2}{16}+\dfrac{y^2}{9} = 1\).
    Ellipse, centre the origin, with x intercepts minus 4 and 4 and y intercepts minus 3 and 3.
    Detailed description
    Assume the top-right corner of the rectangle is at \(X(x, \dfrac{3}{4}\sqrt{16-x^2})\). The area \(A\) of the rectangle \(XYZW\) is given by \[ A = XY \times XW = 2x \times \dfrac{3}{2}\sqrt{16-x^2} = 3x\sqrt{16-x^2}. \] We have \begin{align*} \dfrac{dA}{dx} &= 3\Bigl(\sqrt{16-x^2}-\dfrac{x^2}{\sqrt{16-x^2}}\Bigr) \\ &= 3\Bigl(\dfrac{16-x^2-x^2}{\sqrt{16-x^2}}\Bigr) \\ &= 3\Bigl(\dfrac{16-2x^2}{\sqrt{16-x^2}}\Bigr). \end{align*} So \(\dfrac{dA}{dx}=0\) implies \(x=2\sqrt2\). Furthermore, we have \[ \dfrac{d^2A}{dx^2} = \dfrac{6x(-24+x^2)}{(16-x^2)^{\frac{3}{2}}}, \] and so \(\dfrac{d^2A}{dx^2} <0\) when \(x =2\sqrt2\). The maximum area is \(3\times 2\sqrt 2 \times \sqrt{16-(2\sqrt 2)^2} = 24\). \item The ellipse has equation \[ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1, \] where \(a,b > 0\). Assume that the top-right corner of the rectangle is at \((x,y)\), where \(0 \leq x \leq a\) and \(0 \leq y \leq b\). Let \(A\) be the area of the rectangle. Then \begin{align*} A &= \dfrac{4b}{a}x\sqrt{a^2-x^2} \\ \dfrac{dA}{dx} &= \dfrac{4b(a^2-2x^2)}{a\sqrt{a^2-x^2}}. \end{align*} So \(\dfrac{dA}{dx} = 0\) implies \(x = \dfrac{a}{\sqrt{2}}\). The maximum area is \(2ab\).
Exercise 11

Let the cylinder have radius \(r\) and height \(h\). Here \(r>0\) and \(h>0\), and they are variables. Let the cone have radius \(R\) and height \(H\). They are constants.

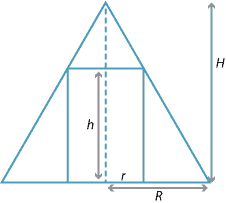
A cross-sectional diagram of a cylinder of radius r and height h placed in a cone of radius R and height H.

The volume \(V\) of the cylinder is given by \[

V = \pi r^2 h.

\] Using similar triangles, we have \begin{align*} \dfrac{H-h}{r} &= \dfrac{H}{R} \\ HR-hR &= rH \\ h &= H-\dfrac{rH}{R}. \end{align*} Substitute for \(h\) in the formula for \(V\): \[ V = \pi r^2\Bigl(H-\dfrac{rH}{R}\Bigr) = \dfrac{\pi H}{R} \bigl( Rr^2 - r^3 \bigr). \] Differentiate with respect to \(r\): \[ \dfrac{dV}{dr} = \dfrac{\pi H}{R} \bigl( 2Rr - 3r^2 \bigr) = \dfrac{\pi H r}{R} \bigl( 2R - 3r \bigr). \] Check for stationary points: \(\dfrac{dV}{dr} = 0\) implies \(r = \dfrac{2R}{3}\), since \(r\neq 0\). The second derivative is \[ \dfrac{d^2V}{dr^2} = \dfrac{\pi H}{R} \bigl( 2R - 6r \bigr). \]

So, when \(r = \dfrac{2R}{3}\), we have \(\dfrac{d^2V}{dr^2} = -2\pi H < 0\). A local maximum occurs when \(r = \dfrac{2R}{3}\). This gives the maximum volume of the cylinder, which is \(V = \dfrac{4\pi R^2H}{27}\).

Exercise 12

The point \(P\) is moving along the curve \(y = \sqrt{x^3+56}\). We have

\[ \dfrac{dy}{dx} = \dfrac{3x^2}{2\sqrt{x^3+56}}, \]

and so

\[ \dfrac{dx}{dt} = \dfrac{dx}{dy} \times \dfrac{dy}{dt} = \dfrac{2\sqrt{x^3+56}}{3x^2} \times \dfrac{dy}{dt}. \]

When \(x=2\), we are given that \(\dfrac{dy}{dt} = 2\), and so

\[ \dfrac{dx}{dt} = \dfrac{2\sqrt{2^3+56}}{3 \times 2^2} \times 2 = \dfrac{8}{3}. \]
Exercise 13

Assume the meteor is a sphere of radius \(r\). Its surface area is \(S = 4\pi r^2\), and its volume is \(V = \dfrac{4}{3} \pi r^3\). The volume is decreasing at a rate proportional to the surface area. That is,

\[ \dfrac{dV}{dt} = -kS = -4\pi k r^2, \]

for some positive constant \(k\). Using the chain rule, we have

\[ \dfrac{dr}{dt} = \dfrac{dr}{dV} \times \dfrac{dV}{dt} = \dfrac{1}{4\pi r^2} \times -4\pi k r^2 = -k. \]

So the radius is decreasing at a constant rate.