Links forward

Finding gradients on a parametric curve

We start with a simple example.

Consider the parametric curve defined by \begin{align*} x &= t^2 \\ y &= t^3. \end{align*} We will find \(\dfrac{dy}{dx}\) in terms of \(t\) by using the chain rule and the result \[ \dfrac{dt}{dx} = \dfrac{1}{\dfrac{dx}{dt}}. \] We have \(\dfrac{dx}{dt} = 2t\) and \(\dfrac{dy}{dt} = 3t^2\). Hence, \begin{align*} \dfrac{dy}{dx} &= \dfrac{dy}{dt} \times \dfrac{dt}{dx} \\ &= \dfrac{3t^2}{2t} \\ &= \dfrac{3t}{2}. \end{align*}

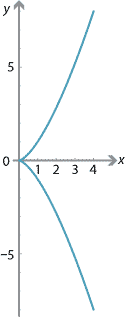
Projectile motion

The motion of a particle projected at an angle \(\alpha\) to the horizontal with an initial velocity of \(u\) m/s can be described by the parametric equations \begin{align*} x &= u\cos(\alpha) t \\ y &= u\sin(\alpha) t - \dfrac{1}{2}gt^2, \end{align*} where \(g\) is the acceleration due to gravity. A method for deriving these equations is given in the module Motion in a straight line. The velocities in the horizontal and vertical directions are \[ \dfrac{dx}{dt} = u\cos(\alpha) \qquad\text{and}\qquad \dfrac{dy}{dt} = u\sin(\alpha) - gt. \] Using the chain rule, we have \[ \dfrac{dy}{dx} = \dfrac{dy}{dt} \times \dfrac{dt}{dx} = \dfrac{u\sin(\alpha) - gt}{u\cos(\alpha)}. \] This gives the gradient of the path of the projectile in terms of \(t\), for \(t \geq 0\). This also allows us to find the angle of inclination of the path of the projectile at any time \(t\). We use the fact that \[ \tan\theta = \dfrac{dy}{dx}, \] where \(\theta\) is the angle of inclination of the path to the horizontal. For example, if \(\alpha = \dfrac{\pi}{4}\) and \(u = 10\), then \[ \tan\theta = \dfrac{\dfrac{10}{\sqrt{2}}-gt}{\dfrac{10}{\sqrt{2}}} = 1 - \dfrac{\sqrt{2}gt}{10}. \]

Cycloids

A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line. For a wheel of radius 1, the parametric equations of the cycloid are

\begin{align*} x &= \theta-\sin\theta \\ y &= 1-\cos\theta. \end{align*}

The graph of \(y\) against \(x\) for \(0\leq \theta\leq 6\pi\) is as follows.

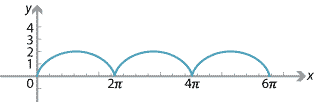
We can find the gradient at a point on the cycloid by using the chain rule. We have

\[ \dfrac{dx}{d\theta} = 1 - \cos\theta \qquad\text{and}\qquad \dfrac{dy}{d\theta} = \sin\theta. \]

The chain rule gives

\begin{align*} \dfrac{dy}{dx} &= \dfrac{dy}{d\theta} \times \dfrac{d\theta}{dx} \\ &= \dfrac{\sin \theta}{1 - \cos\theta} \\ &= \dfrac{2\sin \dfrac{\theta}{2} \cos\dfrac{\theta}{2}}{2\sin^2\dfrac{\theta}{2}} \\ &= \cot\dfrac{\theta}{2}. \end{align*}

Also,

\begin{align*} \dfrac{d^2y}{dx^2} &= \dfrac{d}{dx} \Bigl(\dfrac{dy}{dx} \Bigr) \\ &= \dfrac{d}{dx} \Bigl(\cot\dfrac{\theta}{2}\Bigr) \\ &= \dfrac{d}{d\theta} \Bigl(\cot\dfrac{\theta}{2}\Bigr) \times \dfrac{d\theta}{dx} \\ &= -\dfrac{1}{4\sin^4(\dfrac{\theta}{2})}. \end{align*}

Notes.

• There are stationary points where \(\cot\dfrac{\theta}{2} = 0\), which is equivalent to \(\cos\dfrac{\theta}{2} = 0\). This occurs when \(\theta\) is an odd multiple of \(\pi\), that is, when \(\theta \in \{\dots, -5\pi, -3\pi, -\pi, \pi, 3\pi, 5\pi, \dots\}\). Note that \(\dfrac{d^2y}{dx^2} < 0\) for these values of \(\theta\), and so there are local maxima when \(\theta\) is an odd multiple of \(\pi\).
• The function is not differentiable when \(\theta\) is even multiple of \(\pi\). That is, these are critical points of the function.
• There are no points of inflexion.
• The \(x\)-intercepts occur when \(\cos\theta = 1\), that is, when \(\theta\) is an even multiple of \(\pi\).

Cardioids

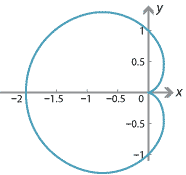
A cardioid is the curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. The cardioid shown in the graph has parametric equations

\begin{align*} x &= (1-\cos t)\cos t \\ y &= (1-\cos t)\sin t. \end{align*}

It is plotted for \(t \in [0,2\pi]\).

We can calculate the gradient of the cardioid for a particular value of \(t\) as follows:

\begin{align*} \dfrac{dx}{dt} &= -\sin t + 2\sin t \cos t = \sin 2t - \sin t \\ \dfrac{dy}{dt} &= \cos t - \cos^2 t + \sin^2 t = \cos t - \cos 2t, \end{align*} and so \[ \dfrac{dy}{dx} = \dfrac{dy}{dt} \times \dfrac{dt}{dx} = \dfrac{\cos t - \cos 2t}{\sin 2t - \sin t}. \]

The gradient is defined for \(\sin 2t - \sin t \neq 0\). For \(t \in [0,2\pi]\), this means that gradient is not defined for \(t = 0, \dfrac{\pi}{3}, \pi, \dfrac{5\pi}{3}, 2\pi\). The corresponding \(x\)-values are \(0, \dfrac{1}{4}, -2, \dfrac{1}{4}, 0\).

There are points of zero gradient when \(t = \dfrac{2\pi}{3}, \dfrac{4\pi}{3}\), which corresponds to \(x = -\dfrac{3}{4}\).

Next page - History and applications