Links forward
Critical points
In the section Graph sketching, we looked at stationary points of a function \(f\), that is, points where \(f'(x)=0\). We gave conditions for a stationary point to be local minimum or a local maximum.
Local maxima and minima also occur in other cases. The point \((c,f(c))\) on the left-hand graph is a local minimum. The point \((d,f(d))\) on the right-hand graph is a local maximum. These are examples of critical points. In each case, the function is not differentiable at that point.
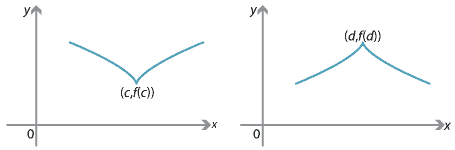
Figure : Examples of critical points.
Definition
A critical point for a function \(f\) is any value of \(x\) in the domain of \(f\) at which \(f'(x) = 0\) or at which \(f\) is not differentiable.
Every stationary point is a critical point.
Not every critical point is a local minimum or maximum point. In the following diagram, the function is not differentiable at the point \((c,f(c))\), since the tangent is vertical. There is a point of inflexion at \((c,f(c))\).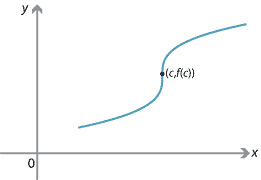
Next page - Links forward - Finding gradients on a parametric curve
