Content

Maxima and minima problems

The need to find local maxima and minima arises in many situations. The first example we will look at is very familiar, and can also be solved without using calculus. Examples of solving such problems without the use of calculus can be found in the module Quadratics .

Example

Find the dimensions of a rectangle with perimeter 1000 metres so that the area of the rectangle is a maximum.

Solution

Let the length of the rectangle be $x$ m, the width be $y$ m, and the area be $A$ m$^2$.

Rectangle with sides x and y.

The perimeter of the rectangle is 1000 metres. So

\[ 1000 = 2x + 2y, \]

and hence

\[ y = 500-x. \]

The area is given by $A = xy$. Thus

\[ A(x) = x(500-x) = 500x - x^2. \qquad (1) \]

Because $x$ and $y$ are lengths, we must have $0 \leq x\leq 500$.

The problem now reduces to finding the value of $x$ in $[0,500]$ for which $A$ is a maximum. Since $A$ is differentiable, the maximum must occur at an endpoint or a stationary point.

From (1), we have

\[ \dfrac{dA}{dx} = 500 - 2x. \]

Setting $\dfrac{dA}{dx}=0$ gives $x=250$.

Hence, the possible values for $A$ to be a maximum are $x=0$, $x=250$ and $x=500$. Since $A(0) = A(500) = 0$, the maximum value of $A$ occurs when $x = 250$.

The rectangle is a square with side lengths 250 metres. The maximum area is $62\ 500$ square metres.

Notes.

$\dfrac{dA}{dx}>0$, for $0\leq x <250$, and $\dfrac{dA}{dx}<0$, for $250<x\leq 500$. Hence, there is a local maximum at $x=250$.
$\dfrac{d^2 A}{dx^2} = -2 < 0$. This is a second way to see that $x=250$ is a local maximum.
The graph of $A(x) = 500x - x^2$ is a parabola with a negative coefficient of $x^2$ and a turning point at $x=250$. This is a third way of establishing the local maximum.
It is worth looking at the graph of $A(x)$ against $x$.

Graph of A(x) = 500x minus x squared

Interactive 1

Exercise 9

A farmer has 8 km of fencing wire, and wishes to fence a rectangular piece of land. One boundary of the land is the bank of a straight river. What are the dimensions of the rectangle so that the area is maximised?

The following steps provide a general procedure which you can follow to solve maxima and minima problems.

Steps for solving maxima and minima problems

Step 1.: Where possible draw a diagram to illustrate the problem. Label the diagram and designate your variables and constants. Note any restrictions on the values of the variables.
Step 2.: Write an expression for the quantity that is going to be maximised or minimised. Eliminate some of the variables. Form an equation for this quantity in terms of a single independent variable. This may require some algebraic manipulation.
Step 3.: If $y = f(x)$ is the quantity to be maximised or minimised, find the values of $x$ for which $f'(x)=0$.
Step 4.: Test each point for which $f'(x)=0$ to determine if it is a local maximum, a local minimum or neither.
Step 5.: If the function $y=f(x)$ is defined on an interval, such as $[a,b]$ or $[0,\infty)$, check the values of the function at the end points.

Example

A square sheet of cardboard with each side $a$ centimetres is to be used to make an open-top box by cutting a small square of cardboard from each of the corners and bending up the sides. What is the side length of the small squares if the box is to have as large a volume as possible?

Solution

Step 1.: Let the side length of the small squares be $x$ cm. The side length of the open box is $(a-2x)$ cm, and the height is $x$ cm. Here $a$ is a constant, and $x$ is the variable we will work with. We must have \[ 0\leq x \leq \dfrac{a}{2}. \]
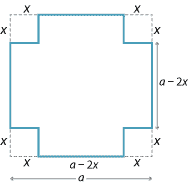
Step 2.: The volume $V$ cm$^3$ of the box is given by \[ V(x) = x(a-2x)^2 = 4x^3-4ax^2+a^2x. \]
Step 3.: We have \[ \dfrac{dV}{dx} = 12x^2- 8ax+a^2 = (2x-a)(6x-a). \] Thus $\dfrac{dV}{dx} = 0$ implies $x=\dfrac{a}{2}$ or $x=\dfrac{a}{6}$.
Step 4.: We note that $x=\dfrac{a}{2}$ is an endpoint and that $V\bigl(\dfrac{a}{2}\bigr)=0$. We will use the second derivative test for $x=\dfrac{a}{6}$. We have \[ \dfrac{d^2V}{dx^2} = 24x-8a = 8(3x-a). \] When $x=\dfrac{a}{6}$, we get \[ \dfrac{d^2V}{dx^2} = 8\Bigl(3 \times \dfrac{a}{6} - a\Bigr) = -4a < 0. \] Hence, $x=\dfrac{a}{6}$ is a local maximum.
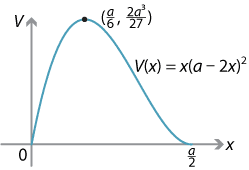
Step 5.: The maximum value of the function is at $x=\dfrac{a}{6}$, as $V(0) = V\bigl(\dfrac{a}{2}\bigr) = 0$. The maximum volume is \[ V\Bigl(\dfrac{a}{6}\Bigr) = \dfrac{2a^3}{27}. \] The following diagram shows the graph of $V$ against $x$.

The following example illustrates a number of issues that can occur.

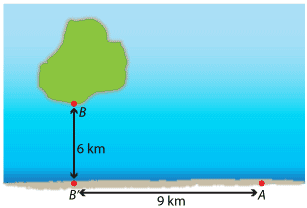
Example

A company wants to run a pipeline from a point $A$ on the shore to a point $B$ on an island which is 6 km from the shore. It costs $\$P$ per kilometre to run the pipeline on shore, and $\$Q$ per kilometre to run it underwater. There is a point $B'$ on the shore so that $BB'$ is at right angles to $AB'$. The straight shoreline is the line $AB'$. The distance $AB'$ is 9 km. Find how the pipeline should be laid to minimise the cost if

$P = 4000$ and $Q = 5000$
$P = 5000$ and $Q = 13\ 000$
$P = 24\ 000$ and $Q = 25\ 000$.

Diagram of island 6 km from point B on the island to point B prime on the shore.
Detailed description

Solution

We will work through most of the problem without assigning values to $P$ and $Q$.

Step 1.

Same diagram as above but with additional point C, x km, from B prime and (9 – x) km from point A.

Suppose that the pipeline leaves the shore $x$ km from $B'$ at a point $C$ between $B'$ and $A$. The distance $AC$ is $(9-x)$ km. By Pythagoras' theorem, the distance $CB$ is $\sqrt{36+x^2}$ km. It is important to note that \[ 0 \leq x\leq 9. \]

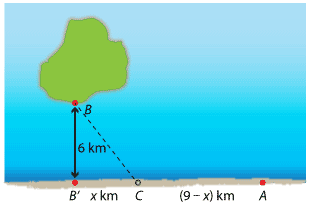
Step 2.

Let $\$T$ be the total cost. Then \[ T(x) = P(9-x)+Q\sqrt{36+x^2}. \qquad (1) \]

Step 3.

We have \[ \dfrac{dT}{dx} = \dfrac{Qx}{\sqrt{36+x^2}} - P. \] Hence, solving $\dfrac{dT}{dx}=0$ gives \begin{align*} \dfrac{Qx}{\sqrt{36+x^2}} - P &= 0 \\ Qx &= P\sqrt{36+x^2} \\ Q^2x^2 &= P^2(36+x^2) \\ (Q^2 - P^2)x^2 &= 36P^2 \\ x &= \sqrt{\dfrac{36P^2}{Q^2 - P^2}} = \dfrac{6P}{\sqrt{Q^2 - P^2}}. \qquad (2) \end{align*} Note that we need $Q>P$ for this solution $x$ to exist, and we also need $0 \leq x \leq 9$. If $Q\leq P$, the pipeline should go directly from $A$ to $B$, with minimum cost $\$3\sqrt{13}Q$.

Step 4.

Using the second derivative test: \[ \dfrac{d^2T}{dx^2} = \dfrac{36 Q}{(36+x^2)^{\frac{3}{2}}} > 0, \] for all $x$. Hence, there is a local minimum at $x = \dfrac{6P}{\sqrt{Q^2 - P^2}}$ for the function with rule $T(x)$. Such a local minimum may occur outside the interval $[0,9]$.

Step 5.

If $x=0$, then $T = 9P+6Q$.
If $x=9$, then $T = 3\sqrt{13}Q$.
If $x=\dfrac{6P}{\sqrt{Q^2-P^2}}$, then from (1) we have \begin{alignat*}{2} T &= P\Bigl(9-\dfrac{6P}{\sqrt{Q^2-P^2}}\Bigr) + Q\sqrt{36+\dfrac{36P^2}{Q^2 - P^2}} \\ &= 9P - \dfrac{6P^2}{\sqrt{Q^2-P^2}} + Q\sqrt{\dfrac{36(Q^2 - P^2) + 36P^2}{Q^2 - P^2}} \\ &= 9P - \dfrac{6P^2}{\sqrt{Q^2-P^2}} + \dfrac{6Q^2}{\sqrt{Q^2-P^2}} \\ &= 9P + 6\sqrt{Q^2-P^2}. &&(3) \end{alignat*}

The local minimum occurs in the interval $[0,9]$ if and only if \[ \dfrac{6P}{\sqrt{Q^2-P^2}}\leq 9. \] We now solve this inequality for the ratio $\dfrac{P}{Q}$, assuming that $Q>P$: \begin{align*} \dfrac{6P}{\sqrt{Q^2-P^2}} \leq 9 \ &\iff\ \dfrac{36P^2}{Q^2 - P^2} \leq 81 \\ &\iff\ 36P^2 \leq 81(Q^2-P^2) \\ &\iff\ 117P^2 \leq 81Q^2 \\ &\iff\ \dfrac{P^2}{Q^2} \leq \dfrac{81}{117}. \end{align*} Thus the local minimum occurs in the interval $[0,9]$ if and only if $\dfrac{P}{Q} \leq \dfrac{3}{\sqrt{13}}$.

We now consider the particular values of $P$ and $Q$ specified in the question.

$P = 4000$ and $Q = 5000$. By equation (1), we have \[ T = 4000(9-x) + 5000\sqrt{36+x^2},\qquad\text{for } 0 \leq x \leq 9. \] Note that \begin{align*} T(0) &= 36\;000+30\;000 = 66\;000 \\ T(9) &= 15\;000\sqrt{13} \approx 54\;083. \end{align*} By equation (2), the local minimum point is $x = 8$ and in this case, by equation (3), the minimum cost is \[ T_{\mathrm{min}} = 9 \times 4000 + 6 \times 3000 = \$54\;000. \]
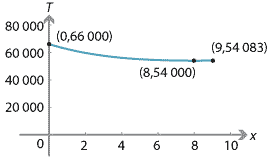
$P = 5000$ and $Q = 13\;000$. By equation (1), we have \[ T = 5000(9-x) + 13\;000\sqrt{36+x^2},\qquad\text{for } 0 \leq x \leq 9. \] We note that \[ T(0) = 123\;000, \qquad T(9) = 39\;000\sqrt{13} \approx 140\;616. \] By equation (2), the local minimum point is $x = \dfrac{5}{2}$ and in this case, by equation (3), the minimum cost is \[ T_{\mathrm{min}} = 9\times 5000 + 6\times 12\;000 = \$117\;000. \]
$P = 24\;000$ and $Q = 25\;000$. By equation (1), we have \[ T = 24\;000(9-x) + 25\;000\sqrt{36+x^2},\qquad \text{for } 0 \leq x \leq 9. \] We note that \[ T(0) = 366\;000, \qquad T(9) = 75\;000\sqrt{13} \approx 270\;416. \] By equation (2), the local minimum occurs at $x = \dfrac{144}{7}$, which is outside the required domain. In fact, we have $\dfrac{dT}{dx} < 0$, for all $x \in [0,9]$. The minimum cost is \[ T(9) = 75\;000\sqrt{13} \approx \$270\;416. \]

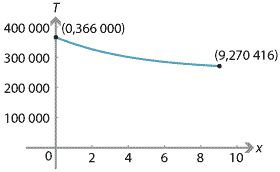
Note. In parts 1 and 2, the minimum occurs at a local minimum. But, in part 3, the minimum occurs at an endpoint.

The following example has reasonably demanding algebra and involves some geometry, but the result is surprisingly neat.

Example

A right cone is circumscribed around a given sphere. Find when its volume is a minimum.

Solution

Step 1.

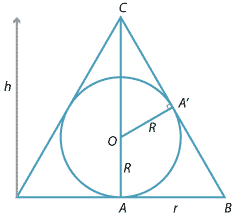
The following diagram shows a vertical cross-section of the cone and sphere.

Cross –sectional diagram of cone containing a sphere.

The sphere has radius $R$, which we treat as a constant. The cone has radius $r$ and height $h$. These are variables. From the geometry, we must have $h>2R>0$ and $r>R>0$. The centre of the sphere is marked by $O$. The radius $OA'$ is drawn perpendicular to $CB$.

Step 2.

We will find $h$ in terms of $r$ and $R$. We begin by noting that $OC = h-R$. By using Pythagoras' theorem in $\triangle OCA',$ we get $CA' =\sqrt{h^2-2hR}$. Since $\triangle CA'O$ is similar to $\triangle CAB$ (AAA), we can write \[ \dfrac{CA'}{CA} = \dfrac{OA'}{BA}. \] Hence, \[ \dfrac{\sqrt{h^2-2hR}}{h} = \dfrac{R}{r}. \] Solving for $h$, we obtain \begin{alignat*}{2} \dfrac{h^2-2hR}{h^2} &= \dfrac{R^2}{r^2} &\qquad&(\text{square both sides}) \\ r^2(h^2-2hR) &= h^2R^2 &&(\text{cross-multiply}) \\ r^2h^2-2hRr^2 &= h^2R^2 \\ r^2h-2Rr^2 &= hR^2 &&(\text{as } h\neq 0) \\ h(r^2-R^2) &= 2r^2R \\ h &= \dfrac{2r^2R}{r^2-R^2}. \end{alignat*} The volume of the cone is given by $V=\dfrac{1}{3}\pi r^2h$. Substituting for $h$, we obtain \[ V = \dfrac{2\pi r^4R}{3(r^2-R^2)}. \] We have now expressed the volume in terms of the one variable $r$.

Step 3.

We have \[ \dfrac{dV}{dr} = \dfrac{4\pi R r^3(r^2-2R^2)}{3(r^2-R^2)^2}. \] So $\dfrac{dV}{dr} =0$ implies that $r^3(r^2-2R^2)=0$, which implies that $r=0$ or $r=\sqrt{2}R$. Clearly, $r = \sqrt{2}R$ is the solution we want.

Step 4.

Using \[ \dfrac{dV}{dr} = \dfrac{4\pi R r^3(r^2-2R^2)}{3(r^2-R^2)^2}, \] we can complete the following gradient diagram.

Value of $r$		$\sqrt{2}R$
Sign of $\dfrac{dV}{dr}$	-	0	+
Slope of graph	$\diagdown$	—	$\diagup$

Alternatively, we can use the second derivative test. We have \[ \dfrac{d^2V}{dr^2} = \dfrac{4\pi R(r^6-3 r^4 R^2+6 r^2 R^4)}{3(r^2-R^2)^3}. \] Substituting $r = \sqrt{2}R$ gives \[ \dfrac{d^2V}{dr^2} = \dfrac{32\pi R}{3} > 0. \] Hence, we have a local minimum at $r = \sqrt{2}R$.
The graph of $V$ against $r$ is as follows. There is a vertical asymptote at $r=R$, and the graph approaches a parabola with equation $V = \dfrac{2\pi R}{3}r^2$ as $r$ becomes very large.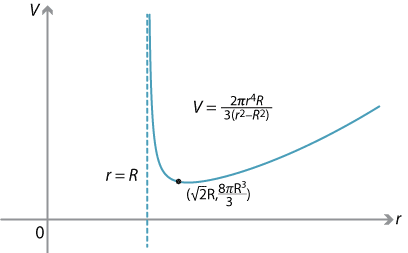

Exercise 10

Find the maximum area of a rectangle that can be inscribed in the ellipse $\dfrac{x^2}{16}+\dfrac{y^2}{9} = 1$. Assume that the sides of the rectangle are parallel to the axes.
Find the maximum area of a rectangle that can be inscribed in the ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1$. Assume that the sides of the rectangle are parallel to the axes.

Exercise 11

A hollow cone has base radius $R$ and height $H$. What is the volume of the largest cylinder that can be placed under it?

Next page - Content - Related rates of change

Value of \(r\)		\(\sqrt{2}R\)
Sign of \(\dfrac{dV}{dr}\)	-	0	+
Slope of graph	\(\diagdown\)	—	\(\diagup\)