Appendix

Functions differentiable and not

We mentioned earlier that not all functions have derivatives. We now say a little more, although a full discussion of these issues is the subject matter of higher level university courses on analysis.

For a function to have a derivative, it must first of all be continuous — you must be able to draw the graph without taking your pen off the page! More rigorously, continuity at a point \(x=a\) means that we must have \(\lim\limits_{x \to a} f(x) = f(a)\).

Roughly speaking, a function will only have a derivative where its graph is smooth, and can be drawn on the page without sharp corners.

For instance, consider the absolute value function

\[ f(x) = |x| = \begin{cases} x &\text{if } x \geq 0, \\ -x &\text{if } x < 0. \end{cases} \]

The following diagram shows the graph of \(y=f(x)\).

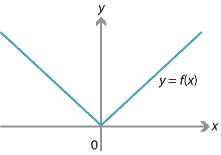
Figure : Graph of \(f(x) = |x|\).

For \(x>0\), we have \(f(x)=x\) and so \(f'(x)=1\). For \(x<0\), we have \(f(x)=-x\) and so \({f'(x)=-1}\). However, at \(x=0\) we have a problem.

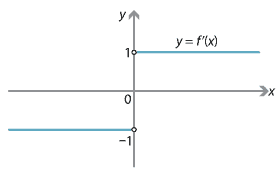
Detailed description
Figure : Graph of \(f'(x)\).

By definition, if \(f'(0)\) were to exist,

\[ f'(0) = \lim_{\Delta x \to 0} \dfrac{f(0+\Delta x) - f(0)}{\Delta x} = \lim_{\Delta x \to 0} \dfrac{|\Delta x|}{\Delta x}. \]

Unfortunately, for any \(\Delta x > 0\) we have \(\dfrac{|\Delta x|}{\Delta x} = 1\), while for any \(\Delta x < 0\) we have \(\dfrac{|\Delta x|}{\Delta x} = -1\). So if \(\Delta x\) approaches 0 from above, the limit is 1, but if \(\Delta x\) approaches 0 from below, the limit is \(-1\). Therefore, the limit does not exist, and \(f'(0)\) is not defined.

The function \(f(x) = |x|\) is therefore differentiable at all \(x \neq 0\), but is not differentiable at \(x=0\). It is differentiable almost everywhere, but not everywhere.

The absolute value function, however, is rather tame in comparison to examples like the following. Consider the infinite series

\[ f(x) = \cos (\pi x) + \dfrac{1}{2} \cos(3\pi x) + \dfrac{1}{2^2} \cos(3^2 \pi x) + \dotsb = \sum_{n=0}^\infty \dfrac{1}{2^n} \cos (3^n \pi x). \]

The following graphs show a few partial sums of this series.

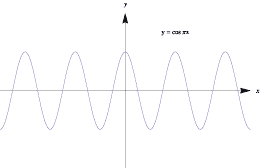
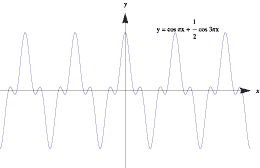
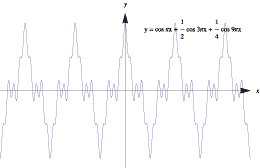
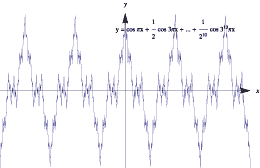
Graphs of approximations to a nowhere-differentiable function.

Note how the functions oscillate more rapidly and the graphs become 'bumpier' as each term is added. In the limit, the function oscillates so wildly that, although it remains continuous, it is too bumpy for the derivative to exist. It can be shown that this function is continuous everywhere, but is differentiable nowhere!

Next page - Answers to exercises