Content

Calculating the gradient of \(y=x^2\)

Let us consider a specific function \(f(x) = x^2\) and its graph \(y=f(x)\), which is the standard parabola. To illustrate the ideas in the previous section, we will calculate the gradient of this curve at \(x=1\).

We first construct secant lines between the points on the graph at \(x=1\) and \(x = 1 + \Delta x\), and calculate their gradients.

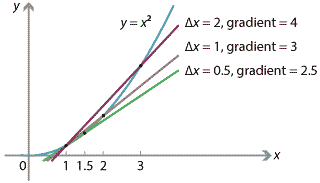
Detailed description
Figure : Gradients of secants from \(x=1\) to \(x = 1 + \Delta x\).

For instance, taking \(\Delta x = 2\), we consider the secant connecting the points at \(x=1\) and \(x=3\). Between these two points, \(f(x)\) increases from \(f(1) = 1\) to \(f(3) = 9\), giving \(\Delta y = 8\), and hence

\[ \dfrac{\Delta y}{\Delta x} = \dfrac{8}{2} = 4. \]

We compute gradients of secants for various values of \(\Delta x\) in the following table.

Secants of the parabola \(f(x) = x^2\)

Secant between points	\(\Delta x\)	\(\Delta y = f(x+\Delta x) - f(x)\)	Gradient of secant \(\dfrac{\Delta y}{\Delta x}\)
\(x=1\),   \(x=3\)	2	8	4
\(x=1\),   \(x=2\)	1	3	3
\(x=1\),   \(x=1.5\)	0.5	1.25	2.5
\(x=1\),   \(x=1.1\)	0.1	0.21	2.1
\(x=1\),   \(x=1.001\)	0.001	0.002001	2.001

As \(\Delta x\) approaches 0, the gradients of the secants approach 2. It turns out that indeed the gradient of the tangent at \(x=1\) is 2. To see why, consider the interval of length \(\Delta x\), from \(x=1\) to \(x=1+\Delta x\). We have

\begin{align*} \Delta y &= f(1+\Delta x) - f(1) \\ &= (1+\Delta x)^2 - 1^2 \\ &= 2\,\Delta x + (\Delta x)^2, \end{align*}

so that

\begin{align*} \dfrac{\Delta y}{\Delta x} &= \dfrac{2\,\Delta x + (\Delta x)^2}{\Delta x} \\ &= 2 + \Delta x. \end{align*}

In the limit, as \(\Delta x \to 0\), we obtain the instantaneous rate of change

\begin{align*} \dfrac{dy}{dx} &= \lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} \\ &= \lim_{\Delta x \to 0} \bigl(2 + \Delta x\bigr) = 2. \end{align*} (So, if you were riding your bike and your position was \(f(x) = x^2\) metres after \(x\) seconds, then your instantaneous velocity after 1 second would be 2 metres per second.)

There's nothing special about the point \(x=1\) or the function \(f(x) = x^2\), as the following example illustrates.

Interactive 1

In the examples so far, we have been given a curve, and we have found the gradient of the curve at one particular point on the curve. But we can also find the gradient at all points simultaneously, as the next section illustrates.

Next page - Content - Definition of the derivative