History and applications

Cauchy and Weierstrass

Prior to the careful analysis of limits and their precise definition, mathematicians such as Euler were experimenting with more and more complicated limiting processes; sometimes finding correct answers — often for wrong reasons — and sometimes finding incorrect ones. A lack of rigour often led to paradoxes of the type we looked in the section Paradoxes of the infinite.

In the early 19th century, the need for a more formal and logical approach was beginning to dawn on mathematicians such as Cauchy and later Weierstrass.

The French mathematician Augustine-Louie Cauchy (pronounced Koshi, with a long o) (1789–1857) was one of the early pioneers in a more rigorous approach to limits and calculus. He was also responsible for the development of complex analysis, which applies the notions of limits and calculus to functions of a complex variable. Many theorems and equations in that subject bear his name. Cauchy is regarded by many as a pioneer of the branch of mathematics known as analysis, although he also made use of infinitesimals.

Analysis may be thought of as the theoretical side of limits and calculus. It is a very important branch of modern mathematics, and teaches us how to deal with calculus in ways that are rigorous and logically valid.

In 1821, Cauchy wrote Cours d'Analyse, which had a great impact on continental mathematics. In it he introduced proofs using the \(\varepsilon\) notation we saw in the section Links forward (Formal definition of a limit).

At roughly the same time, Bernard Bolzano (1781–1848) was attempting to deal with some of the classical paradoxes in his book The paradoxes of the infinite. He was the first to give a rigorous \(\varepsilon\)-\(\delta\) definition of a limit, although much of his work was not widely disseminated at the time.

While Cauchy made mathematicians think more deeply about what they were doing, it was Karl Weierstrass (1815–1897) who is generally regarded as the father of modern analysis. He gave the first rigorous definition of continuity of a function \(f(x)\) at a point \(a\).

The definition states: Given \(\varepsilon > 0\), there is a positive real number \(\delta\) such that, if \(|x-a|<\delta\), then \(|f(x)-f(a)| < \varepsilon\).

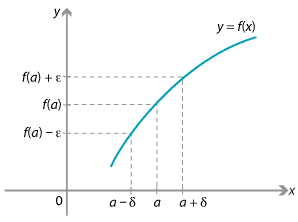
Continuity of \(f(x)\) at \(x = a\).
Detailed description

This basically says that a function \(f(x)\) is continuous at a point \(a\) if \(x\)-values that are close to \(a\) (i.e., within \(\delta\) of \(a\)) get mapped by \(f\) to \(y\)-values that are close to \(f(a)\) (i.e., within \(\varepsilon\) of \(f(a)\)).

In fact, this definition of the continuity of \(f(x)\) at \(a\) says exactly that \(\lim\limits_{x\to a} f(x) = f(a)\), using the formal definition of a limit. So it agrees with our definition of continuity in the section Continuity of piecewise-defined functions.

Weierstrass's work was very influential and formed a solid foundation for analysis for decades to come. He shocked the mathematical world by coming up with a function which is continuous everywhere but differentiable nowhere! That is, its graph could be drawn without lifting the pen, but it is not possible to draw a tangent to the curve at any point on it! The function he gave is expressed in terms of an infinite series of functions:

\[ f(x) = \sum_{n=1}^\infty \dfrac{1}{2^n}\cos(4^n x). \]

The following diagram, created using Mathematica, gives the graph of \(y = \sum\limits_{n=1}^{50} \frac{1}{2^n}\cos(4^n x)\) for \(0\leq x\leq 2\pi\).

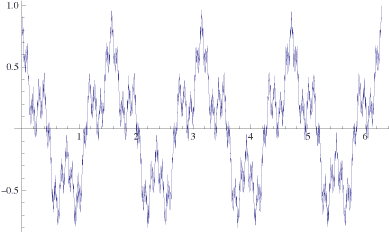
An approximation to Weierstrass's function.
Detailed description

Roughly speaking, this infinite series has trigonometric terms with amplitude \(\dfrac{1}{2^n}\), which quickly approaches 0 as \(n\) gets larger. It is this aspect that is used to prove continuity. It can be formally proven that the infinite series converges for every value of \(x\), and that the function so generated is continuous everywhere. If, however, we were to try to differentiate this function term-by-term, then the derivative of the general term is \(-2^n\sin(4^n x)\) whose amplitude is \(2^n\), which becomes very large as \(n\) increases. So the series of derivatives does not converge. Hence the function is not differentiable anywhere.

Next page - Answers to exercises