Content

Continuity of piecewise-defined functions

Since functions are often used to model real-world phenomena, sometimes a function may arise which consists of two separate pieces joined together. Questions of continuity can arise in these case at the point where the two functions are joined. For example, consider the function

\[ f(x) = \begin{cases} \dfrac{x^2-9}{x-3} &\text{if \(x \neq 3\)}\\\\ 6 &\text{if \(x=3\).} \end{cases} \]

This function is continuous everywhere, except possibly at \(x=3\). We can see whether or not this function is continuous at \(x=3\) by looking at the limit as \(x\) approaches 3. Using the ideas from the section Limit at a point, we can write

\[ \lim_{x\to 3}\dfrac{x^2-9}{x-3} = \lim_{x\to 3}\dfrac{(x-3)(x+3)}{x-3} = 6. \]

Since 6 is also the value of the function at \(x=3\), we see that this function is continuous. Indeed, this function is identical with the function \(f(x) = x+3\), for all \(x\).

Now consider the function

\[ g(x) = \begin{cases} \dfrac{x^2-9}{x-3} &\text{if \(x \neq 3\)}\\\\ 7 &\text{if \(x=3\).} \end{cases} \]

The value of the function at \(x=3\) is different from the limit of the function as we approach 3, and hence this function is not continuous at \(x=3\). We can see the discontinuity at \(x = 3\) in the following graph of \(g(x)\).

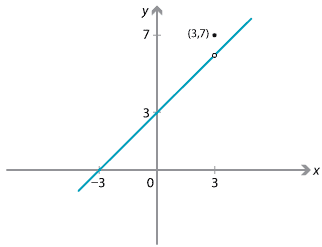
Graph of y equals x plus 3 for x not equal to 3 and point at (3, 7).

We can thus give a slightly more precise definition of a function \(f(x)\) being continuous at a point \(a\). We can say that \(f(x)\) is continuous at \(x = a\) if

Example

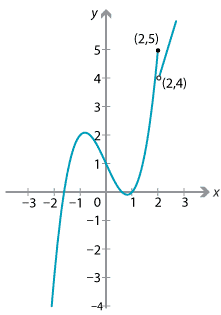
Examine whether or not the function

\[ f(x) = \begin{cases} x^3-2x+1 &\text{if \(x\leq 2\)}\\ 3x-2 &\text{if \(x>2\)} \end{cases} \]

is continuous at \(x=2\).

Solution

Notice that \(f(2) = 2^3-2\times 2+1 = 5\). We need to look at the limit from the right-hand side at \(x=2\). For \(x>2\), the function is given by \(3x-2\) and so

\[ \lim_{x\to 2^+} f(x) = \lim_{x\to 2^+} (3x-2) = 4. \]

In this case, the limit from the right at \(x=2\) does not equal the function value, and so the function is not continuous at \(x=2\) (although it is continuous everywhere else).

Graph of y equals x cubed minus 2x + 1 if x is less than or equal to 2 and y equals 3x minus 2 if x > 2. Closed dot at (2, 5).

Exercise 7

Examine whether or not the function

\[ f(x) = \begin{cases} 4-x^2 &\text{if \(x\leq 0\)}\\ 4+x &\text{if \(x>0\)} \end{cases} \]

is continuous at \(x=0\).

Screencast of exercise 7 mp4 of screencast of exercise 7

Next page - Links forward - Formal definition of a limit