Content

Limit at a point

As well as looking at the values of a function for large values of \(x\), we can also look at what is happening to a function near a particular point.

For example, as \(x\) gets close to the real number 2, the value of the function \(f(x)=x^2\) gets close to 4. Hence we write

\[ \lim_{x\to 2} x^2 = 4. \]

Sometimes we are given a function which is defined piecewise, such as

\[ f(x) = \begin{cases} x+3 &\text{if \(x\leq 2\)}\\ x &\text{if \(x>2\).} \end{cases} \]

The graph of this function is as follows.

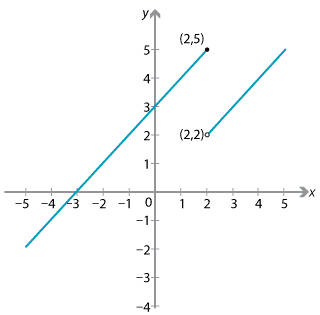
Graph of y equals x plus three if x is less than or equal to 2 and y equals x if x > 2. Closed dot at (2, 5) and open dot at (2, 2).

We can see from the `jump' in the graph that the function does not have a limit at 2:

as the \(x\)-values get closer to 2 from the left, the \(y\)-values approach 5
but as the \(x\)-values get closer to 2 from the right, the \(y\)-values do not approach the same number 5 (instead they approach 2).

In this case, we say that

\[ \lim_{x\to 2} f(x) \text{ does not exist}. \]

Sometimes we are asked to analyse the limit of a function at a point which is not in the domain of the function. For example, the value \(x=3\) is not part of the domain of the function \(f(x) = \dfrac{x^2-9}{x-3}\). However, if \(x \neq 3\), we can simplify the function by using the difference of two squares and cancelling the (non-zero) factor \(x-3\):

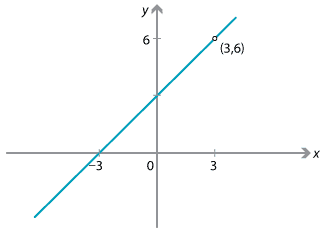
\[ f(x) = \dfrac{x^2-9}{x-3} = \dfrac{(x-3)(x+3)}{x-3} = x+3, \qquad \text{for } x \neq 3. \]

Now, when \(x\) is near the value 3, the value of \(f(x)\) is near \(3+3=6\). Hence, near the \(x\)-value 3, the function takes values near 6. We can write this as

\[ \lim_{x\to 3} \dfrac{x^2-9}{x-3} = 6. \]

The graph of the function \(f(x) = \dfrac{x^2-9}{x-3}\) is a straight line with a hole at the point \((3,6)\).

Graph of y equals x plus 3 with a hole at (3, 6)

Example

Find

\[ \lim_{x\to 2} \dfrac{x^2-3x+2}{x^2-4}. \]

Solution

We cannot substitute \(x=2\), as this produces 0 in the denominator. We therefore factorise and cancel the factor \(x-2\):

\begin{align*} \lim_{x\to 2} \dfrac{x^2-3x+2}{x^2-4} &= \lim_{x\to 2} \dfrac{(x-2)(x-1)}{(x-2)(x+2)}\\ &= \lim_{x\to 2} \dfrac{x-1}{x+2} = \dfrac{1}{4}. \end{align*}

Even where the limit of a function at a point does not exist, we may be able to obtain useful information regarding the behaviour of the function near that point, which can assist us in drawing its graph.

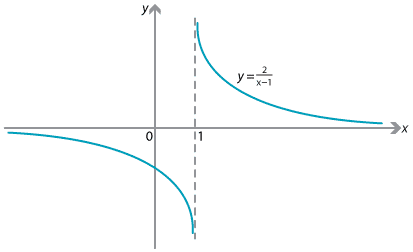
For example, the function

\[ f(x) = \dfrac{2}{x-1} \]

is not defined at the point \(x=1\). As \(x\) takes values close to, but greater than 1, the values of \(f(x)\) are very large and positive, while if \(x\) takes values close to, but less than 1, the values of \(f(x)\) are very large and negative. We can write this as

\[ \dfrac{2}{x-1} \to \infty\ \text{as}\ x\to 1^+ \qquad \text{and} \qquad \dfrac{2}{x-1} \to -\infty\ \text{as}\ x\to 1^-. \]

The notation \({x\to 1^+}\) means that `\(x\) approaches 1 from above' and \({x\to 1^-}\) means `\(x\) approaches 1 from below'.

Thus, the function \(f(x) = \dfrac{2}{x-1}\) has a vertical asymptote at \(x=1\), and the limit as \(x\to 1\) does not exist. The following diagram shows the graph of the function \(f(x)\). The line \(y=0\) is a horizontal asymptote.

Graph of y equals 2 over x minus one. Hyperbola with asymptotes y equals 0 and x equals one.

Exercise 4

Discuss the limit of \(f(x)= \dfrac{x^2}{x^2-1}\) at the points \(x=1\), \(x=-1\) and as \(x\to \pm\infty\).

Exercise 5

Discuss the limit of the function

\[ f(x) = \dfrac{x^2-2x-15}{2x^2+5x-3} = \dfrac{(x-5)(x+3)}{(2x-1)(x+3)} \]

\(x\to \infty\)
\(x\to 5\)
\(x\to -3\)
\(x\to \dfrac{1}{2}\)
\(x\to 0\).

Screencast of exercise 5

Next page - Content - Further examples