Content

Limit of a function at infinity

Just as we examined the limit of a sequence, we can apply the same idea to examine the behaviour of a function \(f(x)\) as \(x\) becomes very large.

For example, the following diagram shows the graph of \(f(x)=\dfrac{1}{x}\), for \(x > 0\). The value of the function \(f(x)\) becomes very small as \(x\) becomes very large.

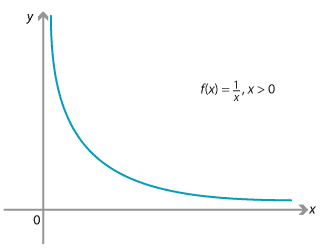
We write

\[ \lim_{x\to \infty} \dfrac{1}{x} = 0. \]

One of the steps involved in sketching the graph of a function is to consider the behaviour of the function for large values of \(x\). This will be covered in the module Applications of differentiation.

The following graph is of the function \(f(x) = \dfrac{2x^2}{1+x^2}\). We can see that, as \(x\) becomes very large, the graph levels out and approaches, but does not reach, a height of 2.

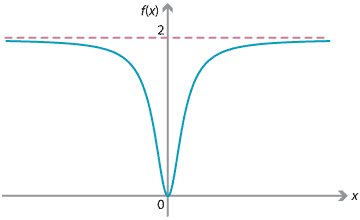
We can analyse this behaviour in terms of limits. Using the idea we saw in the section Limit of a sequence, we divide the numerator and denominator by \(x^2\):

\[ \lim_{x\to \infty} \dfrac{2x^2}{1+x^2} = \lim_{x\to \infty} \dfrac{2}{\dfrac{1}{x^2}+1} = 2. \]

Note that as \(x\) goes to negative infinity we obtain the same limit. That is,

\[ \lim_{x\to -\infty} \dfrac{2x^2}{1+x^2} = 2. \]

This means that the function approaches, but does not reach, the value 2 as \(x\) becomes very large. The line \(y=2\) is called a horizontal asymptote for the function.

Examining the long-term behaviour of a function is a very important idea. For example, an object moving up and down under gravity on a spring, taking account of the inelasticity of the spring, is sometimes referred to as damped simple harmonic motion. The displacement, \(x(t)\), of the object from the centre of motion at time \(t\) can be shown to have the form

\[ x(t) = Ae^{-\alpha t} \sin \beta t, \]

where \(A\), \(\alpha\) and \(\beta\) are positive constants. The factor \(Ae^{-\alpha t}\) gives the amplitude of the motion. As \(t\) increases, this factor \(Ae^{-\alpha t}\) diminishes, as we would expect. Since the factor \(\sin \beta t\) remains bounded, we can write

\[ \lim_{t\to \infty} x(t) = \lim_{t\to \infty} Ae^{-\alpha t} \sin \beta t = 0. \]

In the long term, the object returns to its original position.

Next page - Content - Limit at a point