Content
Limit of a sequence
Consider the sequence whose terms begin
\[ 1, \dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, \dots \]and whose general term is \(\dfrac{1}{n}\). As we take more and more terms, each term is getting smaller in size. Indeed, we can make the terms as small as we like, provided we go far enough along the sequence. Thus, although no term in the sequence is 0, the terms can be made as close as we like to 0 by going far enough.
We say that the limit of the sequence \(\bigl(\, \dfrac{1}{n} : n = 1, 2, 3, \dots \,\bigr)\) is 0 and we write
\[ \lim_{n\to \infty} \dfrac{1}{n} = 0. \]It is important to emphasise that we are not putting \(n\) equal to \(\infty\) in the sequence, since infinity is not a number — it should be thought of as a convenient idea. The statement above says that the terms in the sequence \(\dfrac{1}{n}\) get as close to 0 as we please (and continue to be close to 0), by allowing \(n\) to be large enough.
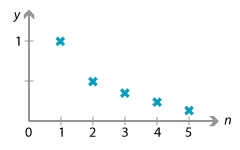
Graph of the sequence \(\dfrac{1}{n}\).
In a similar spirit, it is true that we can write
\[ \lim_{n\to \infty} \dfrac{1}{n^a} = 0, \]for any positive real number \(a\). We can use this, and some algebra, to find more complicated limits.
Example
Find
\[ \lim_{n\to \infty} \dfrac{3n^2+2n+1}{n^2-2}. \]Solution
Intuitively, we can argue that, if \(n\) is very large, then the largest term (sometimes called the dominant term) in the numerator is \(3n^2\), while the dominant term in the denominator is \(n^2\). Thus, ignoring the other terms for the moment, for very large \(n\) the expression \(\dfrac{3n^2+2n+1}{n^2-2}\) is close to 3.
The best method of writing this algebraically is to divide by the highest power of \(n\) in the denominator:
\[ \lim_{n\to \infty} \dfrac{3n^2+2n+1}{n^2-2} = \lim_{n\to \infty} \dfrac{3+\dfrac{2}{n}+\dfrac{1}{n^2}}{1-\dfrac{2}{n^2}}. \]Now, as \(n\) becomes as large as we like, the terms \(\dfrac{2}{n}\), \(\dfrac{1}{n^2}\) and \(\dfrac{2}{n^2}\) approach 0, so we can complete the calculation and write
\begin{align*} \lim_{n\to \infty} \dfrac{3n^2+2n+1}{n^2-2} &= \lim_{n\to \infty} \dfrac{3+\dfrac{2}{n}+ \dfrac{1}{n^2}}{1-\dfrac{2}{n^2}}\\ &= \dfrac{\lim\limits_{n\to \infty} \bigl(3+\dfrac{2}{n}+ \dfrac{1}{n^2}\bigr)}{\lim\limits_{n\to \infty} \bigl(1-\dfrac{2}{n^2}\bigr)}\\ &= \dfrac{3}{1} = 3. \end{align*}Exercise 1
Find
\[ \lim_{n\to \infty} \dfrac{5n^3+(-1)^n}{4n^3+2}. \]Next page - Content - Limiting sums
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |