Answers to exercises
Exercise 1
Substituting \(x=3\) into \(2x^3 - 8x^2 + 7x - 3\) gives
\[ 2 \cdot 3^3 - 8 \cdot 3^2 + 7 \cdot 3 - 3 = 54 - 72 + 21 - 3 = 0. \]Exercise 2
From \(f(x)=2(x-5)^2(x+7)\), we expand to \(f(x)=2x^3 -6x^2 -90x + 350\) and so
\[ f'(x) = 6x^2 - 12x - 90 = 6(x^2 - 2x - 15). \]Therefore \(f'(x)=0\) implies \(x^2 - 2x - 15 = 0\), so \((x-5)(x+3) = 0\) and therefore \(x = 5\) or \(x=-3\). We check that \(f(-3)=512\) and \(f(5)=0\).
Exercise 3
- The graph of \(y=a(x-h)^3 + k\) is obtained from \(y=x^3\) by a dilation of factor \(a\) from the \(x\)-axis in the \(y\)-direction, then a translation of \(h\) units to the right and \(k\) units upwards.
- For example, the graph of \(f(x) = -8(x-3)^3 + 27\) is given below.
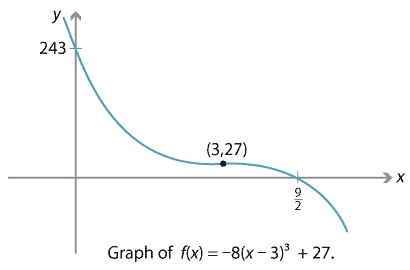
If \(f(x) = a(x-h)^3 + k\), expanding gives \begin{align*} f(x) &= a(x^3 - 3hx^2 + 3h^2 x - h^3) + k \\ &= ax^3 - 3ah x^2 + 3ah^2 x - ah^3 + k. \end{align*} Since \(f(x)\) can also be written as \(ax^3 + bx^2 + cx + d\), then \(b = -3ah\) and \(c=3ah^2\).
Hence \(b^2 - 3ac = (-3ah)^2 - 3a(3ah^2) = 9a^2h^2 - 9a^2 h^2 = 0\). - Almost any example will work. For instance we can take \(f(x) = x^3 + x\). Then \(a=1\), \(b=0\), \(c=1\), so \(b^2 - 3ac = 0 - 3 = -3 \neq 0\).
Exercise 4
A polynomial of even degree has asymptotic behaviour like \(y=a_n x^n\) where \(n\) is even. If \(a_n\) is positive, then as \(x \to \pm \infty\), \(f(x) \to \infty\); if \(a_n\) is negative, then as \(x \to \pm \infty\), \(f(x) \to -\infty\). The graph either begins by going down and ends by going up, or begins by going up and ends by going down. Therefore there must be an odd number of turning points.
On the other hand, a polynomial of odd degree has asymptotic behaviour like \(a_n x^n\) where \(n\) is odd. So \(f(x)\) goes from \(-\infty\) to \(+\infty\) or vice versa. Hence, it either begins and ends by going up, or begins and ends by going down. Therefore there must be an even number of turning points.
Exercise 5
We note that the quartic equation in \(x\) is a quadratic equation in \(x^2\). So let \(z=x^2\), and the equation becomes \(z^2 - 5z + 6 = 0\). Factorising gives \((z-2)(z-3) = 0\), so \(z=2\) or 3. As \(x = \pm \sqrt{z}\), we have the four solutions \(x = \pm \sqrt{2}\), \(\pm \sqrt{3}\).
Exercise 6
Since the coefficients are integers, if there is an integer solution, then it is a factor of 6, i.e., \(\pm 1\), \(\pm 2\), \(\pm 3\) or \(\pm 6\). Substituting these values we find that \(x=-2\) is a solution:
\[ (-2)^3 + 2 (-2)^2 + 3 (-2)+ 6 = -8 + 8 - 6 + 6 = 0. \]Therefore, by the factor theorem, \((x+2)\) is a factor of \(x^3 + 2x^2 + 3x + 6\). Using polynomial division we find
\[ x^3 + 2x^2 + 3x + 6 = (x+2)(x^2 + 3), \]so it remains to find solutions to the quadratic equation \(x^2 +3 = 0\). This quadratic equation has no solutions. Thus the only solution to our original cubic equation is \(x=-2\).
Exercise 7
Since \(r_1\) is a zero of \(f(x)\), we can use the factor theorem to write \(f(x) = (x - r_1)p_1(x)\), for some polynomial \(p_1(x)\). But \(r_2\) is also a zero of \(f(x)\), and so it must be a zero of \((x - r_1)\) or \(p_1(x)\). As \(r_1\) and \(r_2\) are distinct, it follows that \(r_1\) is a zero of \(p_1(x)\). By the factor theorem we have \(p_1(x) = (x - r_2)p_2(x)\), for some polynomial \(p_2(x)\). Thus our original polynomial can now be written as \(f(x) = (x - r_1)(x - r_2)p_2(x)\). Continuing in this way (by considering \(r_3, r_4, \dotsc, r_k\) in turn), it follows that \((x - r_1)(x - r_2) \dotsm (x - r_k)\) is a factor of \(f(x)\).
Exercise 8
Differentiating gives \(f'(x) = 3x^2 + 1\). The stationary points are the solutions of \(3x^2 + 1 = 0\). But this quadratic equation has no real solutions, and so \(f(x)\) has no stationary points.
Exercise 9
We find stationary points by solving \(f'(x) = 0\), i.e., \(3ax^2 + 2bx + c = 0\). This is a quadratic equation and its discriminant is \((2b)^2 - 4(3a)c = 4b^2 - 12ac\), which has the same sign as \(b^2 - 3ac\). When \(b^2 - 3ac < 0\), the discriminant is negative, \(f'(x) = 0\) has no solutions, so there are no stationary points. When \(b^2-3ac = 0\), the discriminant is 0, \(f'(x) = 0\) has precisely one solution and there is one stationary point. When \(b^2 - 3ac > 0\), the discriminant is positive, \(f'(x) = 0\) has two distinct solutions and there are two distinct stationary points.
Exercise 10
The polynomial \(f(x) = x^3 - x\) factorises as \(x(x-1)(x+1)\), so \(x\)-intercepts are at \(x=-1,0,1\). The \(y\)-intercept is \(f(0)=0\). Since the leading term is \(x^3\), as \(x \to \pm \infty\), \(f(x) \to \pm \infty\). The derivative is \(f'(x) = 3x^2 - 1\), so the stationary points can be found by solving the equation \(3x^2 - 1 = 0\), i.e., \(x= \pm \frac{1}{\sqrt{3}}\). We have \(f(-\frac{1}{\sqrt{3}}) = \frac{2}{3\sqrt{3}}\) and \(f(\frac{1}{\sqrt{3}}) = -\frac{2}{3\sqrt{3}}\), so the stationary points are at \((-\frac{1}{\sqrt{3}}, \frac{2}{3\sqrt{3}})\) and \((\frac{1}{\sqrt{3}}, -\frac{2}{3\sqrt{3}})\). We can draw a sign diagram for \(f'(x)\) as follows.
| value of \(x\) | \(−\frac{1}{\sqrt{3}}\) | \(\frac{1}{\sqrt{3}}\) | |||
|---|---|---|---|---|---|
| sign of \(f'(x)\) | + | 0 | − | 0 | + |
| slope of graph \(y=f(x)\) | \(\diagup\) | — | \(\diagdown\) | — | \(\diagup\) |
The graph of \(y=f(x)\) is as shown.
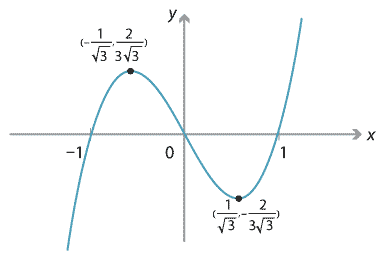
Detailed description of diagram
Exercise 11
Let \(f(x)=x^4-x^2\). Then we may factorise as \(f(x)=x^2(x-1)(x+1)\) and the roots are \(x=0\) (with multiplicity 2) and \(x=-1,1\). As the root at \(x=0\) has multiplicity 2, we have a turning point. Since \(f(0)=0\), the \(y\)-intercept is 0. As the leading term is \(x^4\), the graph of \(f\) is 'happy': \(f(x) \to +\infty\) as \(x \to \pm \infty\). Since \(f'(x) = 4x^3 - 2x = 2x(2x^2-1)\), the stationary points are at \(x=0\) and \(x=\pm \frac{1}{\sqrt{2}}\). We can compute \(f(-\frac{1}{\sqrt{2}}) = -\frac{1}{4}\) and \(f(\frac{1}{\sqrt{2}}) = -\frac{1}{4}\), so the stationary points are \((-\frac{1}{\sqrt{2}},-\frac{1}{4})\), \((0,0)\) and \((\frac{1}{\sqrt{2}},-\frac{1}{4})\). Based on the above we can actually deduce the shape of the graph and see that all stationary points are turning points; alternatively we could draw a sign diagram. The graph is as follows.
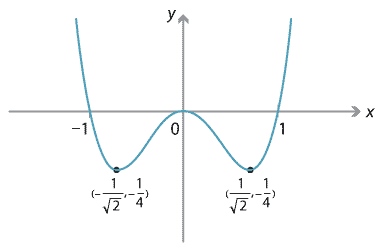
Detailed description of diagram
Exercise 12
The graph is obtained from \(y=x^5\) by reflection in the \(x\)-axis, dilation by factor 4 from the \(x\)-axis in the \(y\)-direction, and translation of 3 to the right and 2 down.
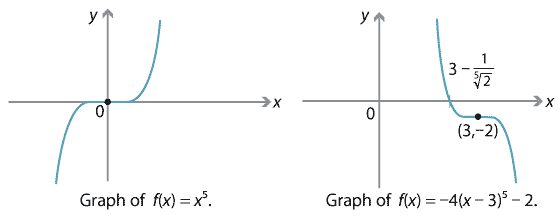
Detailed description of diagrams
Exercise 13
The suggested substitution is \(z = x - 2\). Rewriting the equation in terms of \(z\) gives
\[ (z+2)^3 - 6 (z+2)^2 + 27(z+2) - 58 = 0, \]which simplifies to \(z^3 + 15 z - 20 = 0\). This is now a cubic equation without a quadratic term, which we can rewrite as \(z^3 = 20 - 15z\). To find a solution, following our method, we seek \(A\) and \(B\) such that \(A+B = 20\) and \(3 \sqrt[3]{AB} = -15\), i.e., \(AB = -125\). Substituting \(B = -\frac{125}{A}\) into \(A+B = 20\) gives
\[ A - \frac{125}{A} = 20, \qquad \text{which is equivalent to} \quad A^2 - 20A - 125 = 0. \]This quadratic equation factorises as \((A-25)(A+5) = 0\), so \(A = 25\) or \(-5\), and we obtain a solution \(A=25\), \(B=-5\). Therefore a solution to the cubic equation is \(z = \sqrt[3]{25} - \sqrt[3]{5}\). Substituting back for \(x\) gives a solution \(x = 2 + z = 2 + \sqrt[3]{25} - \sqrt[3]{5}\).
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |