Links forward

Insolvability of quintics

As mentioned earlier, while there is a general method to find the roots of any polynomial up to degree 4 in terms of radical expressions, there is no such general method for polynomials of degree 5 and above. This is the result of theorems discovered independently by Galois and Abel. The topic is well beyond our current scope but we can make a few comments about it.

The theorems of Galois and Abel are in particular about the solvability of polynomial equations in radicals. 'Radical' here refers to the radical sign \(\sqrt[n]{\phantom{i}}\). A radical expression is one that can be built out of integers by the usual operations of addition, subtraction, multiplication, division, and radical signs. When we use radical signs, we are allowed to take square roots, cube roots, fourth roots, and so on — any \(n\)th root where \(n\) is a positive integer. So

\[ \frac{3}{\sqrt{7}} + \sqrt[3]{ \frac{9 - \sqrt{6}}{2 + \sqrt[7]{11} + \sqrt[11]{42} } - \sqrt[3]{2}} \]

is an example of a radical expression, but

\[ \pi + \sqrt{2}, \qquad \log 2, \qquad e^3 \]

are not radical expressions. (So-called 'transcendental functions' \(\sin\), \(\cos\), \(\tan\), \(\log\), \(e^x\) cannot be resolved to radical expressions.) All the solutions we have found to polynomials so far have been radical expressions.

Theorem

The polynomial \(x^5 - 6x + 3\) has no roots which are radical expressions.

Drawing the graph \(y=x^5 - 6x + 3\), we see there are three \(x\)-intercepts. There are roots at approximately \(-1.7\), 0.5 and 1.4. We can see the roots on the real number line — yet the theorem states that these numbers are not radical expressions.

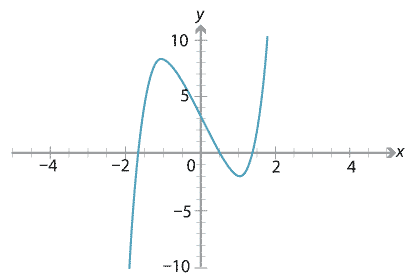
Detailed description of diagram

This example is taken from Ian Stewart's text Galois theory. In fact the same applies to any quintic with rational coefficients and three real roots.

Aside. If we allow the coefficients of our polynomials to be non-radical, then it's easy to make non-radical roots. For example, \(f(x) = x - \pi\) has a root at \(\pi\). Here we are referring to polynomials with integer or rational coefficients.

Next page - Appendix - Lagrange interpolation formula