Content

Solving polynomial equations

Often we need to find the solutions of an equation \(f(x) = 0\), where \(f(x)\) is a polynomial, i.e., the roots of \(f(x)\). This amounts to finding the \(x\)-intercepts of the graph \(y=f(x)\).

When \(f\) is linear or quadratic, solving \(f(x) = 0\) amounts to solving a linear or quadratic equation. We know how to solve these.

For cubics and higher, the question is more difficult. There is a (complicated!) formula for solving cubic equations, containing many \(+\), \(-\), \(\times\), \(\div\) and radical signs (i.e., \(\sqrt{\phantom{i}}\), \(\sqrt[3]{\phantom{i}}\), \(\sqrt[4]{\phantom{i}}\), etc.). There is also a (monstrously complicated!) formula for quartic equations. However, there is no such formula for a solution of a general quintic or higher degree equation. This astonishing fact was proved by Niels Heinrik Abel in 1824, and independently by the extraordinary French mathematician Évariste Galois quoted at the beginning of this module. (For more on the brief, tumultuous and tragic life of Galois, see the History section of this module.) Think about it: How would you go about proving that there is no formula to solve an equation?

The insolvability of quintic polynomials is a university-level topic, although we shall say something about it in the Links forward section. In secondary school mathematics, the only higher degree polynomial equations encountered are ones with simple solutions.

One simple higher degree polynomial equation is \(x^5 = 2\), which obviously has solution \(x = \sqrt[5]{2}\). Another type of simple polynomial equation is found in the following exercise.

For other simple polynomial equations, solutions can be found by educated trial and error. Our next task is to learn the tricks for educated trial and error.

Solving by factorising

Let's suppose we are asked to solve the cubic equation \(x^3-4x^2+2x+3=0\). So we let \(f(x) = x^3 - 4x^2 + 2x + 3\), and we seek the roots of \(f(x)\). We begin finding solutions by trial and error. Of course there are many guesses we could make!

The trick is to guess factors of the constant term. Here the constant term is 3, so we consider factors of 3. We must be careful to check both the positive and negative factors of 3, so we check 1, \(-1\), 3, \(-3\):

\begin{align*} f(1) &= 1^3 - 4 \cdot 1^2 + 2 \cdot 1 + 3 = 1 - 4 + 2 + 3 = 2, \\ f(-1) &= (-1)^3 - 4(-1)^2 + 2(-1) + 3 = -1 -4 -2 + 3 = -4, \\ f(3) &= 3^3 - 4 \cdot 3^2 + 2 \cdot 3 + 3 = 27 - 36 + 6 + 3 = 0, \\ f(-3) &= (-3)^3 - 4 (-3)^2 + 2(-3) + 3 = -27 - 36 - 6 + 3 = -66. \end{align*}

We have found a solution \(x=3\).

Now, as soon as we have a solution, we can factorise \(f(x)\). Specifically, when we have a solution \(x=a\), then \((x-a)\) is a factor of \(f(x)\). In the present case, \(x=3\) is a solution, so \((x-3)\) is a factor. We can use polynomial division to do this factorisation.

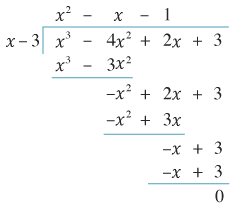
Detailed description of diagram

(Recall how polynomial long division works, following the above example. We start from the \(x-3 \mid x^3 - 4x^2 + 2x + 3\). Dividing the \(x\) into the leading \(x^3\) gives \(x^2\). Multiplying down \(x^2\) by \(x-3\) gives \(x^3 - 3x^2\), which we then subtract from \(x^3 - 4x^2+2x+3\) to obtain \(-x^2+2x+3\). Dividing \(x\) into \(-x^2\) gives \(-x\); then multiplying down \(-x\) by \(x-3\) gives \(-x^2+3x\). We proceed until we arrive at the remainder of 0.)

Thus \(f(x) = (x-3)(x^2-x-1)\) and we must solve \((x-3)(x^2 - x - 1)=0\). If the product of two numbers is zero, then one of them must be zero. As \(x-3=0\) only has the solution \(x=3\), it remains to solve \(x^2 - x - 1 = 0\), which is just a quadratic equation. Completing the square we have

\[ \Big( x - \frac{1}{2} \Big)^2 - \frac{5}{4} = 0, \qquad\text{so}\quad x = \frac{1}{2} \pm \frac{\sqrt{5}}{2}. \]

We now have all solutions to \(f(x) = 0\). The complete set of solutions is

\[ x = 3, \quad \frac{1}{2} + \frac{\sqrt{5}}{2}, \quad \text{or} \quad \frac{1}{2} - \frac{\sqrt{5}}{2}. \]

To make clear how the 'tricks' used here work, we state them as theorems.

Theorem

Let \(f(x) = a_n x^n + a_{n-1} x^{n-1} + \dots + a_0\) be a polynomial where all the coefficients \(a_0, \dots, a_n\) are integers. Then any integer solution to the equation \(f(x)=0\) must be a factor (positive or negative) of the constant term \(a_0\).

Proof

• Suppose \(k\) is an integer solution, so \(f(k)=0\). Thus we have \[ a_n k^n + a_{n-1} k^{n-1} + \dots + a_1 k + a_0 = 0, \] and each \(a_i\) is an integer. Now every term with a \(k\) in it is a multiple of \(k\) — that's every term on the left-hand side other than the constant term. But the terms on the left-hand side have to add up to 0, so the final term \(a_0\) must be a multiple of \(k\) as well. That is, \(k\) is a factor of \(a_0\).

  \(\Box\)

Theorem (Factor theorem)

Let \(f(x)\) be a polynomial with real coefficients. If \(a\) is a real number such that \(f(a)=0\), then \((x-a)\) is a factor of \(f(x)\).

Proof

• We can perform polynomial division, dividing \(f(x)\) by \((x-a)\), to obtain a quotient \(q(x)\) and a remainder \(r\) which is just a constant. (When you divide by a linear polynomial, you get a constant remainder.) This means that \[ f(x) = (x-a) q(x) + r. \] Now substituting \(x=a\) into the above gives \(f(a) = 0 + r\). As \(f(a)=0\), this means the remainder \(r\) is 0. Thus \(f(x)=(x-a)q(x)\), and \((x-a)\) is a factor of \(f(x)\).

  \(\Box\)

Screencast of exercise 6

Number of solutions

We know that a linear equation \(ax+b=0\) always has one solution \(x=-\dfrac{b}{a}\). On the other hand, a quadratic equation \(ax^2+bx+c=0\) may have zero, one or two real solutions.

For instance, the equation \(x^2 + 1 = 0\) has no real solutions; while \(x^2 - 2x + 1 = 0\) has only one real solution ('repeated twice') since it factorises to \((x-1)^2 = 0\).

The quadratic formula tells us that the number of solutions of a quadratic equation \({ax^2+bx+c=0}\) is determined by the discriminant \(b^2 - 4ac\). There are zero, one or two solutions depending on whether \(b^2 - 4ac\) is negative, zero or positive.

For general polynomials, we can state the following.

Theorem

Let \(f(x)\) be a polynomial of degree \(n\). Then \(f(x)=0\) has at most \(n\) distinct real solutions.

Proof

• Suppose instead that there were more than \(n\) distinct solutions. Let \(n+1\) of these distinct solutions be \(r_1, r_2, \dots, r_{n+1}\). It follows from the factor theorem that the polynomial \((x-r_1)(x-r_2)\dotsm (x-r_{n+1})\) is a factor of \(f(x)\). (See Exercise 7.) Thus \[ f(x) = (x-r_1)(x-r_2) \dotsm (x-r_{n+1}) q(x), \] for some polynomial \(q(x)\). But now the right-hand side has degree at least \(n+1\), while \(f(x)\) has degree \(n\). This is a contradiction, and so \(f(x)\) can have at most \(n\) distinct solutions.

  \(\Box\)

The above theorem is equivalent to saying that the graph \(y=f(x)\) of a polynomial \(f(x)\) of degree \(n\) has at most \(n\) \(x\)-intercepts. So we have proved Conjecture 1 from the previous section.

It turns out that if we allow square roots of negative numbers, leading to the complex numbers, then we can always find \(n\) solutions (counting multiple roots) to an equation of degree \(n\). This is called the fundamental theorem of algebra. See the Appendix for details.

Next page - Content - Behaviour of polynomials at infinity