Links forward

Adding waves

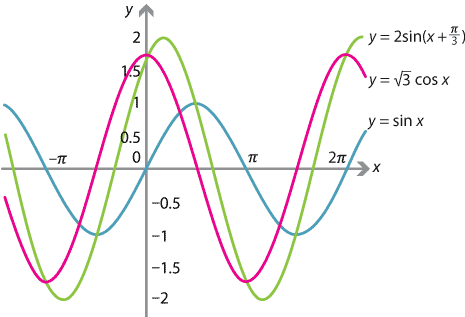
We can add together a sine and a cosine curve. Their sum can be obtained graphically by adding the \(y\)-values of the two curves. It turns out that, if the waves have the same period, this will produce another trigonometric graph with a change in amplitude and a phase shift. Physically, this is called superimposing one wave with another.

This can also be done algebraically. For example, to add \(\sin x\) and \(\sqrt{3}\cos x\), we proceed as follows. Divide their sum by \(\sqrt{1^2 + (\sqrt{3})^2} = 2\), so

\[ \sin x + \sqrt{3}\cos x = 2\Biggl(\dfrac{1}{2}\sin x + \dfrac{\sqrt{3}}{2}\cos x\Biggr). \]

This looks a little like the expansion \(\sin(x+ \alpha) = \sin x\,\cos \alpha + \cos x\,\sin \alpha\). We thus equate \(\cos \alpha = \dfrac{1}{2}\) and \(\sin \alpha = \dfrac{\sqrt{3}}{2}\), which implies that \(\alpha = \dfrac{\pi}{3}\). Hence

\[ \sin x + \sqrt{3}\cos x = 2\sin\Bigl(x+ \dfrac{\pi}{3}\Bigr). \]

The new wave has amplitude 2 and a phase shift of \(\dfrac{\pi}{3}\) to the left.

In general, the same method will work to add \(a\sin x + b\cos x\), in which case we divide out by \(\sqrt{a^2+b^2}\).

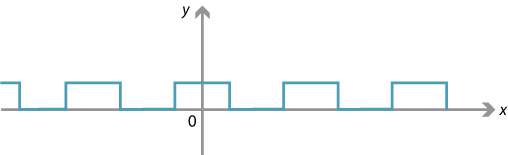
Waves such as the square wave and the saw-tooth wave, which arise in physics and engineering, can be approximated using the sum of a large number of waves — this is the study of Fourier series, which is central to much of modern electrical engineering and technology.

The following square wave is the graph of the function with rule

\[ \dfrac{1}{2} + \dfrac{2}{\pi}\cos x - \dfrac{2}{3\pi}\cos 3x + \dfrac{2} {5\pi}\cos 5x - \dotsb = \dfrac{1}{2} + \dfrac{2}{\pi}\sum_{n=1}^\infty \dfrac{\sin \dfrac{n\pi}{2}}{n}\cos nx. \]

Next page - Links forward - The t formulas