Content

Radian measure

The measurement of angles in degrees goes back to antiquity. It may have arisen from the idea that there were roughly 360 days in a year, or it may have arisen from the Babylonian penchant for base 60 numerals. In any event, both the Greeks and the Indians divided the angle in a circle into 360 equal parts, which we now call degrees. They further divided each degree into 60 equal parts called minutes and divided each minute into 60 seconds. An example would be \(15^\circ22'16''\). This way of measuring angles is very inconvenient and it was realised in the 16th century (or even before) that it is better to measure angles via arc length.

We define one radian, written as \(1^c\) (where the \(c\) refers to circular measure), to be the angle subtended at the centre of a unit circle by a unit arc length on the circumference.

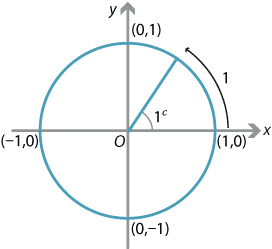
Circle with radius of 1, with centre the origin. Angle in first quadrant showing one radian.
Definition of one radian.

Since the full circumference of a unit circle is \(2\pi\) units, we have the conversion formula

\[ 360^\circ = 2\pi\text{ radians} \] or, equivalently, \[ 180^\circ = \pi\text{ radians}. \]

So one radian is equal to \(\dfrac{180}{\pi}\) degrees, which is approximately \(57.3^\circ\).

Since many angles in degrees can be expressed as simple fractions of 180, we use \(\pi\) as a basic unit in radians and often express angles as fractions of \(\pi\). The commonly occurring angles \(30^\circ\), \(45^\circ\) and \(60^\circ\) are expressed in radians respectively as \(\dfrac{\pi}{6}\), \(\dfrac{\pi}{4}\) and \(\dfrac{\pi}{3}\).

Example

Express in radians:

  1. \(135^\circ\)
  2. \(270^\circ\)
  3. \(100^\circ\).

Solution

  1. \(135^\circ = 3\times 45^\circ = \dfrac{3\pi}{4}^c\)
  2. \(270^\circ = 3\times 90^\circ = \dfrac{3\pi}{2}^c\)
  3. \(100^\circ = \dfrac{100 \pi}{180}^c = \dfrac{5\pi}{9}^c\)
Note. We will often leave off the \(c\), particularly when the angle is expressed in terms of \(\pi\).

Students should have a deal of practice in finding the trigonometric functions of angles expressed in radians. Since students are more familiar with degrees, it is often best to convert back to degrees.

Example

Find

  1. \(\cos \dfrac{4\pi}{3}\)
  2. \(\sin \dfrac{7\pi}{6}\)
  3. \(\tan \dfrac{5\pi}{4}\).

Solution

  1. \(\cos \dfrac{4\pi}{3} = \cos 240^\circ = -\cos 60^\circ = -\dfrac{1}{2}\)
  2. \(\sin \dfrac{7\pi}{6} = \sin 210^\circ = -\sin 30^\circ = -\dfrac{1}{2}\)
  3. \(\tan \dfrac{5\pi}{4} = \tan 225^\circ = \tan 45^\circ = 1\)
Note. You can enter radians directly into your calculator to evaluate a trigonometric function at an angle in radians, but you must make sure your calculator is in radian mode. Students should be reminded to check what mode their calculator is in when they are doing problems involving the trigonometric functions.

Arc lengths, sectors and segments

Measuring angles in radians enables us to write down quite simple formulas for the arc length of part of a circle and the area of a sector of a circle.

In any circle of radius \(r\), the ratio of the arc length \(\ell\) to the circumference equals the ratio of the angle \(\theta\) subtended by the arc at the centre and the angle in one revolution.

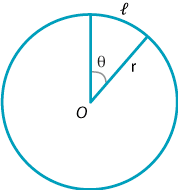
Circle of radius r and centre O showing a sector with angle theta at the centre.

Thus, measuring the angles in radians,

\begin{alignat*}{2} & & \dfrac{\ell}{2\pi r} &= \dfrac{\theta}{2\pi}\\ &\implies\ & \ell &= r\theta. \end{alignat*}

It should be stressed again that, to use this formula, we require the angle to be in radians.

Example

In a circle of radius 12 cm, find the length of an arc subtending an angle of \(60^\circ\) at the centre.

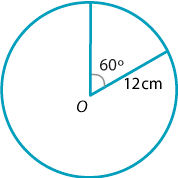
Circle with radius of 12 cm, sector with angle at origin of 60 degrees.

Solution

With \(r=12\) and \(\theta = 60^\circ = \dfrac{\pi}{3}\), we have

\[ \ell = 12\times \dfrac{\pi}{3} = 4\pi \approx 12.57\text{ cm}. \]

It is often best to leave your answer in terms of \(\pi\) unless otherwise stated.

We use the same ratio idea to obtain the area of a sector in a circle of radius \(r\) containing an angle \(\theta\) at the centre. The ratio of the area \(A\) of the sector to the total area of the circle equals the ratio of the angle in the sector to one revolution.

Thus, with angles measured in radians,

\begin{alignat*}{2} & & \dfrac{A}{\pi r^2} &= \dfrac{\theta}{2\pi}\\ &\implies\ & A &= \dfrac{1}{2} r^2\theta. \end{alignat*}

The arc length and sector area formulas given above should be committed to memory.

Example

In a circle of radius 36 cm, find the area of a sector subtending an angle of \(30^\circ\) at the centre.

Solution

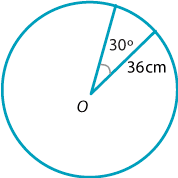
Circle with radius of 36 cm, sector with angle at origin of 30 degrees.

With \(r=36\) and \(\theta = 30^\circ = \dfrac{\pi}{6}\), we have

\[ A = \dfrac{1}{2}\times 36^2\times \dfrac{\pi}{6} = 108\pi\text{ cm}^2. \]

As mentioned above, in problems such as these it is best to leave your answer in terms of \(\pi\) unless otherwise stated.

The area \(A_s\) of a segment of a circle is easily found by taking the difference of two areas.

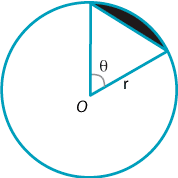
Circle with radius r and sector with angle at the centre theta. Segment formed is shaded.

In a circle of radius \(r\), consider a segment that subtends an angle \(\theta\) at the centre. We can find the area of the segment by subtracting the area of the triangle (using \(\dfrac{1}{2}ab\,\sin\theta\)) from the area of the sector. Thus

\[ A_s = \dfrac{1}{2}r^2\theta - \dfrac{1}{2}r^2\sin \theta = \dfrac{1}{2}r^2(\theta - \sin \theta). \]

Example

Find the area of the segment shown.

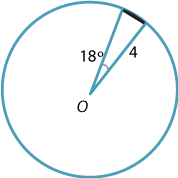
Circle with radius of 4cm, sector with angle at origin of 18 degrees, segment shaded.

Solution

With \(r=4\) and \(\theta = 18^\circ = \dfrac{18\pi}{180} = \dfrac{\pi}{10}\), we have

\[ A_s = \dfrac{1}{2}\times 4^2\times \Bigl(\dfrac{\pi}{10} - \sin\dfrac{\pi}{10}\Bigr)\approx 0.041. \]

Exercise 15

Around a circle of radius \(r\), draw an inner and outer hexagon as shown in the diagram.

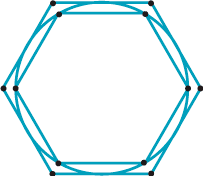
Circle with exterior hexagon and an interior hexagon.

By considering the perimeters of the two hexagons, show that \(3 \leq \pi \leq 2\sqrt{3}\).

Summary of arc, sector and segment formulas
Length of arc \(\ell = r\theta\)
Area of sector \(A=\dfrac{1}{2}r^2\theta\)
Area of segment \(A=\dfrac{1}{2}r^2(\theta-\sin\theta)\)

Solving trigonometric equations in radians

The basic steps for solving trigonometric equations, when the solution is required in radians rather than degrees, are unchanged. Indeed, it is sometimes best to find the solution(s) in degrees and convert to radians at the end of the problem.

Example

Solve each equation for \(0 \leq x \leq 2\pi\):

  1. \(\cos x = -\dfrac{1}{2}\)
  2. \(\sin 3x = 1\)
  3. \(4\cos^2 x + 4\sin x =5\).

Solution

  1. Since \(\cos 60^\circ = \dfrac{1}{2}\), the related angle is \(60^\circ\). The angle \(x\) could lie in the second or third quadrant, so \(x = 180^\circ - 60^\circ\) or \(x = 180^\circ + 60^\circ\). Therefore \(x = 120^\circ\) or \(x = 240^\circ\). In radians, the solutions are \(x = \dfrac{2\pi}{3}, \dfrac{4\pi}{3}\).
  2. Since \(\sin\dfrac{\pi}{2} = 1\), the related angle is \(\dfrac{\pi}{2}\). Since \(x\) lies between 0 and \(2\pi\), it follows that \(3x\) lies between 0 and \(6\pi\). Thus
    \begin{align*} 3x &= \dfrac{\pi}{2},\ 2\pi + \dfrac{\pi}{2},\ 4\pi + \dfrac{\pi}{2}\\ &= \dfrac{\pi}{2},\ \dfrac{5\pi}{2},\ \dfrac{9\pi}{2}. \end{align*}
    Hence \(x= \dfrac{\pi}{6},\ \dfrac{5\pi}{6},\ \dfrac{3\pi}{2}\).
  3. In this case, we replace \(\cos^2 x\) with \(1-\sin^2 x\) to obtain the quadratic
    \begin{alignat*}{2} & & 4(1-\sin^2 x) + 4\sin x &= 5\\ &\implies\ & 4\sin^2 x - 4\sin x +1 &= 0. \end{alignat*}
    This factors to \((2\sin x -1)^2=0\) and so \(\sin x = \dfrac{1}{2}\). In the given range, this has solutions \(x= 30^\circ, 150^\circ\). So, in radians, the solutions are \(x = \dfrac{\pi}{6}, \dfrac{5\pi}{6}\).

Next page - Content - Graphing the trigonometric functions