Content

The sine and cosine rules

The sine rule

In the module Further trigonometry (Year 10), we introduced and proved the sine rule, which is used to find sides and angles in non-right-angled triangles.

Triangle, line segment AB = c, AC = b and BC = a.

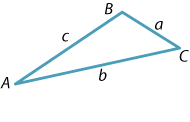
In the triangle \(ABC\), labelled as shown, we have

\[ \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}. \]

Clearly, we may also write this as

\[ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}. \]

In general, one of the three angles may be obtuse. The formula still holds true, although the geometric proof is slightly different.

Exercise 4

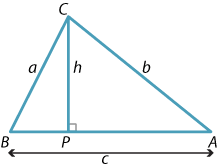
  1. Find two expressions for \(h\) in the diagram below, and hence deduce the sine rule.

    Triangle ABC, AB = c, AC = b, BA = a. Point P on line AB such that CP is perpendicular to AB.
    Detailed description of diagram
  2. Repeat the method of part (a), using the following diagram, to show that the sine rule holds in obtuse-angled triangles.

    Triangle ABC, AB = c, BC = a, AC = b. Triangle AMC, right angle triangle, line CM marked as h, line AC marked as b.

Example

The triangle \(ABC\) has \(AB = 9\text{ cm}\), \(\angle ABC = 76^\circ\) and \(\angle ACB = 58^\circ\).

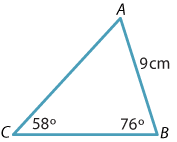
Triangle ABC dash, AB = 9, AC dash = 7. Angle ABC dash = 45 degrees.

Find, correct to two decimal places,

  1. \(AC\)
  2. \(BC\).

Solution

  1. Applying the sine rule gives \[ \dfrac{AC}{\sin 76^\circ} = \dfrac{9}{\sin 58^\circ} \] and so \begin{align*} AC = \dfrac{9 \sin 76^\circ}{\sin 58^\circ}\\ \approx 10.30\text{ cm} \qquad \text{(to two decimal places).} \end{align*}
  2. To find \(BC\), we first find the angle \(\angle CAB\) opposite it. \begin{align*} \angle CAB = 180^\circ - 58^\circ - 76^\circ\\ = 46^\circ. \end{align*} Thus, by the sine rule, \[ \dfrac{BC}{\sin 46^\circ} = \dfrac{9}{\sin58^\circ} \] and so \[ BC \approx 7.63\text{ cm} \qquad \text{(to two decimal places).} \]

The ambiguous case

In the module Congruence (Year 8), it was emphasised that, when applying the SAS congruence test, the angle in question has to be the angle included between the two sides. For example, the following diagram shows two non-congruent triangles \(ABC\) and \(ABC'\) having two pairs of matching sides and sharing a common (non-included) angle.

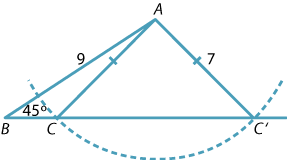
Triangle ABC dash, AB = 9, AC dash = 7. Angle ABC dash = 45 degrees.
Detailed description of diagram

Suppose we are told that a triangle \(PQR\) has \(PQ = 9\), \(\angle PQR = 45^\circ\) and \(PR = 7\). Then the angle opposite \(PQ\) is not uniquely determined. There are two non-congruent triangles that satisfy the given data.

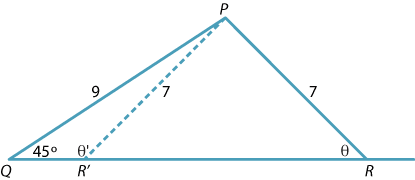
Triangle PQR dash, PQ = 9, PR dash = 7. Angle PQR dash = 45 degrees. Triangle PQR, PQ = 9, PR = 7.
Detailed description of diagram

Applying the sine rule to the triangle, we have

\[ \dfrac{\sin \theta}{9} = \dfrac{\sin 45^\circ}{7} \] and so \begin{align*} \sin\theta = \dfrac{9\sin 45^\circ}{7}\\ \approx 0.9091. \end{align*}

Thus \(\theta \approx 65^\circ\), assuming that \(\theta\) is acute. But the supplementary angle is \(\theta' \approx 115^\circ\). The triangle \(PQR'\) also satisfies the given data. This situation is sometimes referred to as the ambiguous case.

Since the angle sum of a triangle is \(180^\circ\), in some circumstances only one of the two angles calculated is geometrically valid.

The cosine rule

We know from the SAS congruence test that a triangle is completely determined if we are given two sides and the included angle. However, if we know two sides and the included angle in a triangle, the sine rule does not help us determine the remaining side or the remaining angles.

The second important formula for general triangles is the cosine rule.

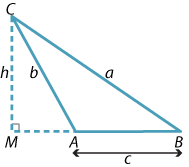
Suppose \(ABC\) is a triangle and that the angles \(A\) and \(C\) are acute. Drop a perpendicular from \(B\) to the line interval \(AC\) and mark the lengths as shown in the following diagram.

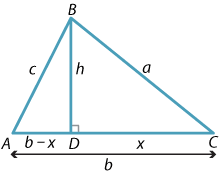
Triangle ABC, BC = a, CA = b, AB = c. Triangle ABD, right angle triangle, AB = c, BD = h, AD = b-x.
Detailed description of diagram

In the triangle \(ABD\), applying Pythagoras' theorem gives

\[ c^2 = h^2 + (b - x)^2. \]

Also, in the triangle \(BCD\), another application of Pythagoras' theorem gives

\[ h^2 = a^2 - x^2. \]

Substituting this expression for \(h^2\) into the first equation and expanding,

\begin{align*} c^2 = a^2 - x^2 + (b - x)^2\\ = a^2 - x^2 + b^2 - 2bx + x^2\\ = a^2 + b^2 - 2bx. \end{align*}

Finally, from triangle \(BCD\), we have \(x = a\,\cos C\) and so

\[ c^2 = a^2 + b^2 - 2ab\,\cos C. \]

This last formula is known as the cosine rule.

Notice that, if \(C = 90^\circ\), then since \(\cos C = 0\) we obtain Pythagoras' theorem, and so we can regard the cosine rule as Pythagoras' theorem with a correction term.

The cosine rule is also true when the angle \(C\) is obtuse. But note that, in this case, the final term in the formula will produce a positive number, because the cosine of an obtuse angle is negative. Some care must be taken in this instance.

By relabelling the sides and angles of the triangle, we can also write the cosine rule as \(a^2 = b^2 + c^2 - 2bc\,\cos A\) and \(b^2 = a^2 + c^2 - 2ac\,\cos B\).

Example

Find the value of \(x\) to one decimal place.

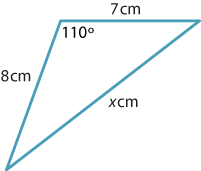
Triangle, measurement of sides given as 7 cm, 8cm, and xcm, angle created by 7cm side and 8cm side given as 110 degrees.

Solution

Applying the cosine rule gives

\begin{align*} x^2 = 7^2 + 8^2 - 2 \times 7 \times 8 \times \cos 110^\circ\\ = 113 + 112\cos70^\circ\\ \approx 151.306, \end{align*}

so \(x \approx 12.3\) (to one decimal place).

Finding angles

If the three sides of a triangle are known, then the three angles are uniquely determined. (This is the SSS congruence test.) Again, the sine rule is of no help in finding the three angles, since it requires the knowledge of (at least) one angle, but we can use the cosine rule instead.

We can substitute the three side lengths \(a\), \(b\), \(c\) into the formula \(c^2 = a^2 + b^2 - 2ab\,\cos C\), where \(C\) is the angle opposite the side \(c\), and then rearrange to find \(\cos C\) and hence \(C\).

Alternatively, we can rearrange the formula to obtain

\[ \cos C = \dfrac{a^2+b^2-c^2}{2ab} \]

and then substitute. Students may choose to rearrange the cosine rule or to learn this further formula. Using this form of the cosine rule often reduces arithmetical errors.

Recall that, in any triangle \(ABC\) labelled as shown, if \(a < b\), then \(\text{angle } A < \text{angle } B\).

Triangle ABC, AC = b, CB = a, AB = c.

Example

A triangle has side lengths 6 cm, 8 cm and 11 cm. Find the smallest angle in the triangle.

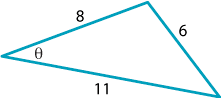
Triangle, lengths of sides given as 8, 6, and 11, angle created by sides with lengths 8 and 11 marked as theta.

Solution

The smallest angle in the triangle is opposite the smallest side.

Applying the cosine rule:

\begin{align*} 6^2 = 8^2 + 11^2 - 2 \times 8 \times 11 \times \cos \theta \\ \cos\theta = \dfrac{8^2+11^2-6^2}{2\times 8 \times 11}\\ =\dfrac{149}{176}. \end{align*}

So \(\theta \approx 32.2^\circ\) (correct to one decimal place).

The area of a triangle

We saw in the module Introductory trigonometry (Years 9--10) that, if we take any triangle with two given sides \(a\) and \(b\) about a given (acute) angle \(\theta\), then the area of the triangle is

\[ \text{Area} = \dfrac{1}{2} ab\,\sin\theta. \]

This formula also holds when \(\theta\) is obtuse.

Exercise 5

A triangle has two sides of length 5 cm and 4 cm containing an angle \(\theta\). Its area is 5 cm\(^2\). Find the two possible (exact) values of \(\theta\) and draw the two triangles that satisfy the given information.

Exercise 6

Write down two different expressions for the area of a triangle \(ABC\) and derive the sine rule from them.

Next page - Content - Trigonometric identities