Content

The four quadrants

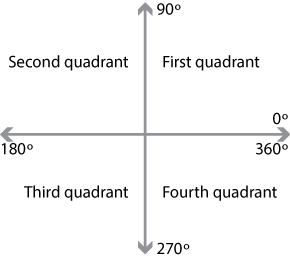
The coordinate axes divide the plane into four quadrants, labelled first, second, third and fourth as shown. Angles in the third quadrant, for example, lie between \(180^\circ\) and \(270^\circ\).

Illustration of coordinate axes with quadrants labelled one, two, three, four.

By considering the \(x\)- and \(y\)-coordinates of the point \(P\) as it lies in each of the four quadrants, we can identify the sign of each of the trigonometric ratios in a given quadrant. These are summarised in the following diagrams.

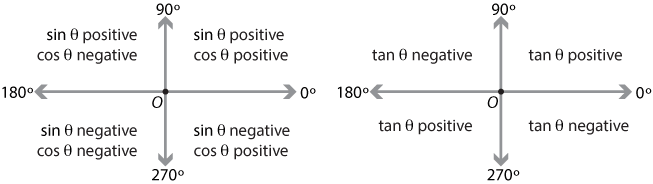
Two illustrations of coordinate axes. Four quadrants identified with the sign of each of the trigonometric ratios in a given quadrant.
Detailed description of diagram

Related angles

In the module Further trigonometry (Year 10), we saw that we could relate the sine and cosine of an angle in the second, third or fourth quadrant to that of a related angle in the first quadrant. The method is very similar to that outlined in the previous section for angles in the second quadrant.

We will find the trigonometric ratios for the angle \(210^\circ\), which lies in the third quadrant. In this quadrant, the sine and cosine ratios are negative and the tangent ratio is positive.

To find the sine and cosine of \(210^\circ\), we locate the corresponding point \(P\) in the third quadrant. The coordinates of \(P\) are \((\cos 210^\circ, \sin 210^\circ)\). The angle \(POQ\) is \(30^\circ\) and is called the related angle for \(210^\circ\).

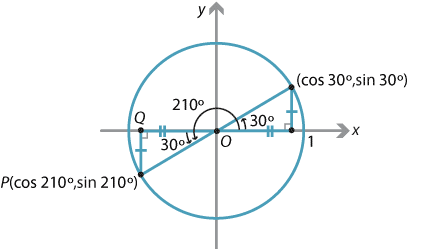
Circle with radius of 1, centre of circle at origin O. Point marked on circle in quadrant 1 as (cos 30 degrees, sin 30 degrees).
Detailed description of diagram

So,

\[ \cos 210^\circ = -\cos 30^\circ = -\dfrac{\sqrt 3}{2} \qquad \text{and} \qquad \sin 210^\circ = -\sin 30^\circ = -\dfrac{1}{2}. \]

Hence

\[ \tan 210^\circ = \tan 30^\circ = \dfrac{1}{\sqrt{3}}. \]

In general, if \(\theta\) lies in the third quadrant, then the acute angle \(\theta - 180^\circ\) is called the related angle for \(\theta\).

Exercise 2

  1. Use the method illustrated above to find the trigonometric ratios of \(330^\circ\).
  2. Write down the related angle for \(\theta\), if \(\theta\) lies in the fourth quadrant.

The basic principle for finding the related angle for a given angle \(\theta\) is to subtract \(180^\circ\) from \(\theta\) or to subtract \(\theta\) from \(180^\circ\) or \(360^\circ\), in order to obtain an acute angle. In the case when the related angle is one of the special angles \(30^\circ\), \(45^\circ\) or \(60^\circ\), we can simply write down the exact values for the trigonometric ratios.

In summary, to find the trigonometric ratio of an angle between \(0^\circ\) and \(360^\circ\):

Example

Use the related angle to find the exact value of

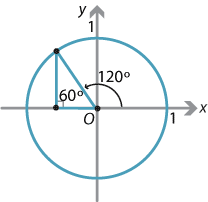
  1. \(\sin 120^\circ\)
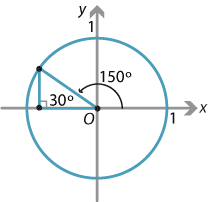
  2. \(\cos 150^\circ\)
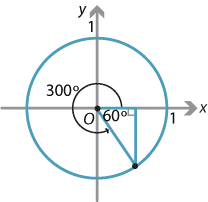
  3. \(\tan 300^\circ\)
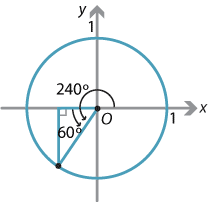
  4. \(\cos 240^\circ\).

Solution

  1. The angle \(120^\circ\) is in the second quadrant, and its related angle is \(60^\circ\).
    So \(\sin 120^\circ = \sin 60^\circ = \dfrac{\sqrt 3}{2}\).

    Circle with radius of 1, centre of circle at origin O. Right-angled triangle, in second quadrant angle marked as 60 degrees.
    Detailed description of diagram

  2. \(\cos 150^\circ = -\cos 30^\circ = -\dfrac{\sqrt 3}{2}\)

    Circle with radius of 1, centre of circle at origin O. Right-angled triangle, in second quadrant angle marked as 30 degrees.
    Detailed description of diagram

  3. \(\tan 300^\circ = -\tan 60^\circ = -\sqrt 3\)

    Circle with radius of 1, centre of circle at origin O. Right-angled triangle, in fourth quadrant angle marked as 60 degrees.
    Detailed description of diagram

  4. \(\cos 240^\circ = -\cos 60^\circ = -\dfrac{1}{2}\)

    Circle with radius of 1, centre of circle at origin O. Right-angled triangle, in third quadrant angle marked as 60 degrees.
    Detailed description of diagram

Exercise 3

Find the exact value of

  1. \(\sin 210^\circ\)
  2. \(\cos 315^\circ\)
  3. \(\tan 150^\circ\).

Screencast of exercise 3 mp4 of screencast of exercise 3

Next page - Content - The sine and cosine rules