Answers to exercises

Exercise 1

1. Assume that \(f \colon \mathbb{R} \to \mathbb{R}\) is both even and odd. Let \(x \in \mathbb{R}\). Since \(f\) is even, we have \(f(-x) = f(x)\), and since \(f\) is odd, we have \(f(-x) = -f(x)\). Therefore \(f(x) = -f(x)\), which implies that \(f(x)=0\). So \(f\) is constant zero.
2. Consider a polynomial \(f(x) = a_0 + a_1x + a_2x^2 + \dots + a_nx^n\). We will assume that \(n\) is even. (The case that \(n\) is odd is similar.) Take \begin{align*} g(x) &= a_0 + a_2x^2 + a_4x^4 + \dots + a_nx^n \\ h(x) &= a_1x + a_3x^3 + a_5x^5 + \dots + a_{n-1}x^{n-1}. \end{align*} Then \(f(x) = g(x)+h(x)\), with \(g(x)\) an even function and \(h(x)\) an odd function.
3. Suppose \[ f(x) = g(x)+h(x)\qquad\qquad (1) \] such that \(g(x)\) is odd and \(h(x)\) is even. Then \begin{align*} f(-x) &= g(-x)+h(-x) \\ &= -g(x)+h(x). \qquad (2) \end{align*} Adding equations (1) and (2) gives \(f(x) + f(-x) = 2h(x)\), and we obtain \[ h(x) = \dfrac{f(x)+f(-x)}{2} \qquad\text{and}\qquad g(x)=\dfrac{f(x)-f(-x)}{2}. \] This gives us the uniqueness of \(g(x)\) and \(h(x)\). We can easily check that the function \(g(x)\) defined this way actually is an odd function, and similarly that \(h(x)\) actually is an even function.

Exercise 2

1. If \(f_1\) and \(f_2\) are odd functions, then \[ (f_1+f_2)(-x) = f_1(-x)+f_2(-x) = -f_1(x)-f_2(x) = -(f_1+f_2)(x), \] so \(f_1+f_2\) is odd. If \(g_1\) and \(g_2\) are even functions, then \[ (g_1+g_2)(-x)=g_1(-x)+g_2(-x)=g_1(x)+g_2(x)=(g_1+g_2)(x), \] so \(g_1+g_2\) is even.
2. Suppose \(f_1\) and \(f_2\) are even, and \(g_1\) and \(g_2\) are odd. If \(h = f_1f_2\), then \[ h(-x) = f_1(-x)\,f_2(-x) = f_1(x)\,f_2(x) = h(x), \] so \(h\) is even. If \(j = g_1g_2\), then \[ j(-x) = g_1(-x)\,g_2(-x) = -g_1(x)\times -g_2(x) = g_1(x)\,g_2(x) = j(x), \] so \(j\) is even. If \(k = f_1g_1\), then \[ k(-x) = f_1(-x)\,g_1(-x) = f_1(x)\times -g_1(x) = -f_1(x)\,g_1(x) = -k(x), \] so \(k\) is odd.
3. Let \(f \colon D \to \mathbb{R}\) with \(f(a) \neq 0\), for some \(a \in D\), and let \(g \colon D \to \mathbb{R}\) with \(g(b) \neq 0\), for some \(b \in D\). Assume that \(f\) is odd and \(g\) is even. Then \begin{alignat*}{2} (f+g)(-a) &= f(-a) + g(-a) \\ &= -f(a) + g(a) &\qquad&\text{since } f \text{ is odd and } g \text{ is even} \\ &\neq f(a) + g(a) &&\text{since } f(a) \neq 0 \\ &= (f+g)(a). \end{alignat*} So \(f+g\) is not even. Similarly, we can use \(b\) to show that \(f+g\) is not odd.

Exercise 3

Let \(y = x^2+4x+10 = (x+2)^2+6\). To map \(y=x^2\) to \(y=(x+2)^2+6\), translate it 2 units to the left and 6 units up.

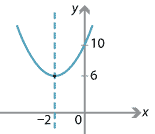
Exercise 4

1. First assume that \(f\) is even. Then \(f(-x)=f(x)\), for all \(x\) in the domain. So reflection in the \(y\)-axis maps \(y=f(x)\) to \(y=f(-x)=f(x)\).

   For the converse, assume that \(y=f(x)\) is mapped to itself under reflection in the \(y\)-axis. Then \(y=f(-x)\) is \(y=f(x)\). Thus \(f(-x)=f(x)\), for all \(x\) in the domain of \(f\), and so \(f\) is even.

2. Note that \(y=f(x)\) is mapped to \(y=-f(x)\) by reflection in the \(x\)-axis, which is then mapped to \(y=-f(-x)\) by reflection in the \(y\)-axis. If the resulting graph is \(y=f(x)\), then \(f(x)=-f(-x)\), for all \(x\) in the domain of \(f\), and so \(f\) is odd. Check the converse.

Exercise 5

1. Let \(g(x) = x-7\). Then \begin{align*} f(g(x)) &= f(x-7) = x-7+7 = x \\ g(f(x)) &= g(x+7) = x+7-7 = x, \end{align*}

   for all \(x\). Hence, \(f\) and \(g\) are inverses of each other.

2. Let \(g(x) = \dfrac{x-5}{4}\). Then \begin{align*} f(g(x)) &= f\Bigl(\dfrac{x-5}{4}\Bigr) = 4\times \Bigl(\dfrac{x-5}{4}\Bigr) + 5 = x \\ g(f(x)) &= g(4x+5) = \dfrac{4x+5-5}{4} = x. \end{align*}

   Thus \(f\) and \(g\) are inverses of each other.

Exercise 6

1. Note that \(\mathrm{domain}(f) = \mathrm{range}(f) = \mathbb{R}\) and \(\mathrm{domain}(g) = \mathrm{range}(g) = \mathbb{R}\). We have \begin{align*} (f\circ g)(x) &= f(g(x)) = f(x^{\dfrac{1}{5}}) = (x^{\dfrac{1}{5}})^5 = x \\ (g\circ f)(x) &= g(f(x)) = g(x^5) = (x^5)^{\dfrac{1}{5}} = x, \end{align*} for all \(x \in \mathbb{R}\). Thus \(f \circ g = \mathrm{id}\) and \(g\circ f = \mathrm{id}\), as required.
2. Let \(f(x) = x^3+2\). We have \(x^3=f(x)-2\) and so \(x=\sqrt[3]{f(x)-2}\). Take \(g(x) = \sqrt[3]{x-2}\). This gives \(f\circ g = \mathrm{id}\) and \(g\circ f = \mathrm{id}\), as required.

Exercise 7

The function \(f(x)=3x+2\) has graph \(y=3x+2\). To find the inverse, we swap \(x\) and \(y\). This gives

\begin{align*} x &= 3y+2 \\ y &= \dfrac{x-2}{3}. \end{align*}

Thus the inverse is given by \(f^{-1}(x) = \dfrac{x-2}{3}\). To find where the two lines meet, we solve \(f(x) = f^{-1}(x)\). This gives

\begin{align*} 3x+2 &= \dfrac{x-2}{3} \\ 9x+6 &= x-2 \\ x &= -1. \end{align*}

Substituting \(x = -1\) into \(y = 3x+2\) yields \(y=-1\). Hence, they meet on the line \(y=x\).

Exercise 8

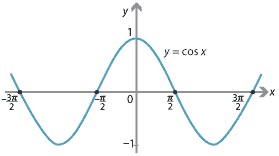
1. Consider the graph of \(y = \cos x\).
   
   We must restrict the domain of \(\cos x\) so that, for each \(c\) with \(-1\leq c\leq 1\), there is exactly one value of \(x\) such that \(\cos x=c\). We restrict the domain of \(\cos x\) to the interval \([0,\pi]\). This gives us a strictly decreasing function with domain \([0,\pi]\) and range \([-1,1]\). The inverse function \(\cos^{-1} x\) has domain \([-1,1]\) and range \([0,\pi]\).
   So \(\cos^{-1} a = b\) if and only if \(\cos b = a\), for \(a \in [-1,1]\), \(b\in [0,\pi]\).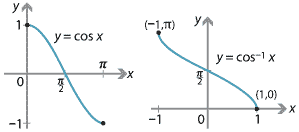
   
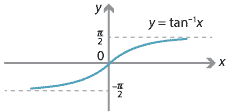
2. Consider the graph of \(y=\tan x\).
   
   We restrict the domain of \(\tan x\) to the interval \((-\dfrac{\pi}{2},\dfrac{\pi}{2})\). This gives us a strictly increasing function with domain \((-\dfrac{\pi}{2},\dfrac{\pi}{2})\) and range \(\mathbb{R}\). The inverse function \(\tan^{-1} x\) has domain \(\mathbb{R}\) and range \((-\dfrac{\pi}{2},\dfrac{\pi}{2})\). So \(\tan^{-1} a = b\) if and only if \(\tan b = a\), for \(a \in \mathbb{R}\), \(b\in (-\dfrac{\pi}{2},\dfrac{\pi}{2})\).