Example

Find

\[ \int_1^2 \log_e x \;dx. \]

Solution

Detailed description

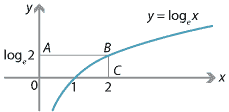
We note that \(e^x\) and \(\log_e x\) are inverses of each other. From the diagram, we have

\begin{align*} \int_1^2 \log_e x \;dx &= \text{Area of rectangle }OABC - \int_0^{\log_e 2} e^y \,dy \\ &= 2\log_e 2 - \bigl[ e^y \bigr]_0^{\log_e 2} \\ &= 2\log_e 2 - 1. \end{align*}