Content
Composites of functions
In this section, for convenience and simplicity, we will focus our attention on functions with domain and codomain the reals.
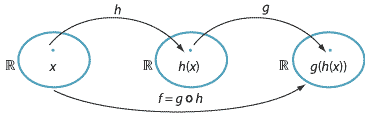
Without worrying about technicalities such as domains and ranges, we can imagine applying one function \(h\) to a real number and then applying another function \(g\) to the image. The result of this is called the composite or the composition of the two functions \(h\) and \(g\). In the above diagram, we can write
\[ f(x) = g(h(x)). \]A common notation for this situation is \(f = g \circ h\).
For example, consider the two functions \(h(x)=x+3\) and \(g(x)=\sin x\), and let \(f = g\circ h\). Then
\[ f(x) = g(h(x)) = g(x+3) = \sin(x+3). \]What if we swap the order and look at \(j = h\circ g\)? We have
\[ j(x) = h(g(x)) = h(\sin x) = \sin(x) + 3. \]Clearly, \(\sin(x+3) \neq \sin(x) + 3\), for any value of \(x\).
Thus the order in which we compose two functions is important.
Notes.
- Throughout this module, we shall assume that if we have an expression involving a trigonometric function, then the variables are measured in radians. Check that your calculator is in radian mode by verifying that \(\sin(2) + 3 \approx 3.9093\).
- The rule \(a+b=b+a\), for all real numbers \(a,b\), is the commutative law for addition. The fact that we can have \(g\circ h \neq h\circ g\), for some functions \(g,h\), says that composition of functions is not commutative.
- Composition of functions is not the same as multiplication of functions: \begin{alignat*}{3} f &= h\circ g &\qquad&\text{means}\qquad& f(x) &= h(g(x)) \\ j &= h\cdot g &\qquad&\text{means}\qquad& j(x) &= h(x)\,g(x). \end{alignat*} So, for example, if \(g(x)=x^2\) and \(h(x)=\sin x\), then \(f(x)=\sin(x^2)\) and \(j(x)=x^2\sin x\). Clearly, \(h \cdot g = g \cdot h\), since \(h(x)\,g(x)=g(x)\,h(x)\) for all \(x\).
- It is possible to compose more than two functions. In particular, if \(f(x)=k(h(g(x)))\), then \(f = k\circ h\circ g\).
- For all functions \(k,h,g\), we have \((k \circ h)\circ g = k\circ (h \circ g)\). So composition of functions is associative. This allows us to write \(k\circ h\circ g\) without any ambiguity.
Example
Let \(g(x)=x^2\), \(h(x)=x+2\) and \(j(x)=\sin x\). Write down the formula for \(k = j\circ h\circ g\).
Solution
We have
\begin{align*} g(x) &= x^2 \\ h(g(x)) &= x^2 + 2 \\ j(h(g(x))) &= \sin(x^2+2). \end{align*}So \(k(x)=\sin(x^2+2)\).
Example
Write
\[ f(x) = \dfrac{1}{\cos(7 \log_2(x^2+3))} \]as the composite of six functions.
Solution
Let
\begin{align*} f_1(x) &= x^2 \\ f_2(x) &= x+3 \\ f_3(x) &= \log_2 x \\ f_4(x) &= 7x \\ f_5(x) &= \cos x \\ f_6(x) &= \dfrac{1}{x}. \end{align*}Then
\[ f = f_6\circ f_5\circ f_4\circ f_3\circ f_2\circ f_1. \]We can compose functions whose domains are subsets of the real numbers. Consider functions \(g \colon A \to \mathbb{R}\) and \(h \colon B \to \mathbb{R}\), where \(A \subseteq \mathbb{R}\) and \(B \subseteq \mathbb{R}\). Then \(g(h(x))\) is defined for each \(x\) in the domain of \(h\) such that \(h(x)\) is in the domain of \(g\). So we obtain a composite function \(g \circ h \colon C \to \mathbb{R}\) with domain \(C = \{\, x \in B : h(x) \in A \,\}\).
For example, consider the functions \(g \colon \mathbb{R}^+ \to \mathbb{R}\) and \(h \colon [0,\pi] \to \mathbb{R}\) given by \(g(x) = \log_e x\) and \(h(x) = \cos x\). Then the composite function \(g \circ h\) is given by \((g \circ h)(x) = \log_e(\cos x)\), with domain \(\{\, x \in [0,\pi] : \cos x \in \mathbb{R}^+ \,\} = [0, \dfrac{\pi}{2})\).
Next page - Content - Geometric transformations of graphs of functions
