Content

Odd and even functions

For most functions \(f(x)\), replacing \(x\) with \(-x\) changes the function dramatically. For some functions, however, there is either no change or just a change in sign. For example, if \(f(x)=x^6\), then \(f(-x)=x^6\). On the other hand, if \(f(x)=x^7\), then \(f(-x)=-x^7\). The notion of odd and even functions generalises these two examples.

Definitions

Example

  1. The polynomial function \(f(x) = x^2+x^4+x^6\) is even.
  2. The polynomial function \(f(x) = x+x^3+x^5\) is odd.
  3. The polynomial function \(f(x)=1+x+x^2\) is neither odd nor even.
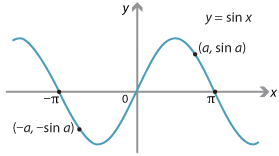
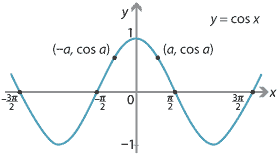
  4. We observe that \[ \sin(-x) = -\sin x \qquad\text{and}\qquad \cos(-x) = \cos x, \] for all \(x\). Thus \(\sin x\) is an odd function and \(\cos x\) is an even function. The function \(\tan x\) is also an odd function, but on a slightly restricted domain: all reals except the odd multiples of \(\dfrac{\pi}{2}\).
  5. The functions \(f(x) = e^x\) and \(g(x) = \log_e x\) are neither odd nor even functions.

Notes. It follows from the definition that, if a function \(f\) is odd or even, then its domain must be symmetric about the origin. That is, it follows that \(x\) is in the domain of \(f\) if and only if \(-x\) is in the domain of \(f\).

Exercise 1
  1. Show that the only function \(f \colon \mathbb{R} \to \mathbb{R}\) which is both odd and even is the constant function \(f(x) = 0\).
  2. Show that every polynomial \(f(x) = a_0 + a_1x + a_2x^2 + \dots + a_{n-1}x^{n-1} + a_nx^n\) can be written as the sum of an odd function and an even function.
  3. Show that every function \(f \colon \mathbb{R} \to \mathbb{R}\) can be written as the sum of an odd function and an even function in a unique way.
Exercise 2

Prove the following:

  1. The sum of two odd functions is odd, and the sum of two even functions is even.
  2. The product of two even functions is even, the product of two odd functions is even, and the product of an odd function and an even function is odd.
  3. Let \(f\) and \(g\) be functions on the same domain, and assume that each function takes at least one non-zero value. If \(f\) is odd and \(g\) is even, then the sum \(f + g\) is neither odd nor even.

Symmetries of odd and even functions

We have observed that \(\cos x\) is an even function. From the following figure, we can see that its graph \(y = \cos x\) is symmetric about the \(y\)-axis. That is, it has reflection symmetry about the \(y\)-axis. Every even function has this property.

Graph of y = cos x. Points (a, cos a) and (-a, cos a) marked.

We have also observed that \(\sin x\) is an odd function. Its graph \(y = \sin x\) has rotational symmetry through \(180^\circ\) about the origin. Every odd function has this property.

Graph of y = sin x. Points (a, sin a) and (-a, -sin a) marked.

Next page - Content - Composites of functions