Links forward

Functions between finite sets

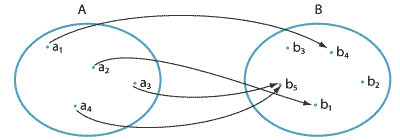
If \(A\) and \(B\) are finite sets, then a function from \(A\) to \(B\) can be specified by listing all elements in \(A\) and their images in \(B\). For example, if

\[ A = \{a_1,a_2,a_3,a_4\} \qquad\text{and}\qquad B = \{b_1,b_2,b_3,b_4,b_5\}, \] then we can define a function \(f\colon A\to B\) by \[ f(a_1)=b_4, \quad f(a_2)=b_1, \quad f(a_3)=b_5 \quad\text{and}\quad f(a_4)=b_5. \]

This can be represented by an arrow diagram.

Set A with points, a1, a2, a3, a4 and set B with points, b1, b2,b3, b4 and b5.
Detailed description

For this example, we have \(\mathrm{domain}(f)=A\), \(\mathrm{codomain}(f)=B\) and \(\mathrm{range}(f)=\{b_1,b_4,b_5\}\).

Exercise 8

Suppose \(|A|=m\) and \(|B|=n\). How many functions are there from \(A\) to \(B\)?

Next page - Links forward - More examples of functions