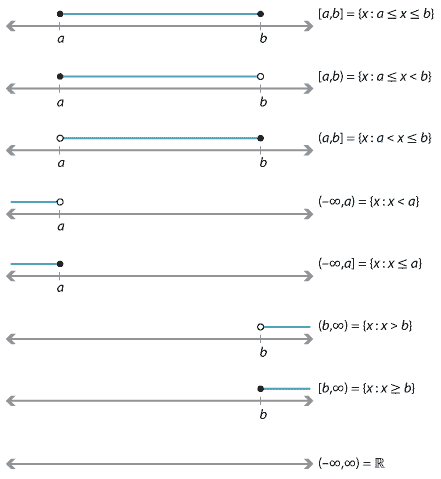Content

Domains and ranges

Recall our six example functions:

For the first four functions, we can take \(x\) to be any real number. That is, we can substitute any \(x\)-value into the formula to obtain a unique \(y\)-value. We therefore say that the natural domain of the functions \(y=x+2\), \(y=3x^2-7\), \(y=\sin x\) and \(y=2^x\) is the set of all real numbers, denoted by \(\mathbb{R}\). On the other hand, for the function \(y=\dfrac{1}{x}\), we cannot substitute \(x=0\); the set of allowable values of \(x\) is all non-zero reals.

Definition

The set of allowable values of \(x\) is called the natural domain of the function.

The natural domain is sometimes called the maximum domain; it is often simply called the domain of the function.

For example:

In a similar way, we can ask: What are all possible values of \(y\), as \(x\) varies over the domain of the function? This set of values is called the range of the function.

The domains and ranges for our six standard examples are given in the following table.

Example functions
Function Domain Range
\(y=x+2\) \(\mathbb{R}\) \(\mathbb{R}\)
\(y=3x^2-7\) \(\mathbb{R}\) \(\{\, y : y\geq -7 \,\}\)
\(y=\sin x\) \(\mathbb{R}\) \(\{\, y : -1\leq y\leq 1 \,\}\)
\(y=2^x\) \(\mathbb{R}\) \(\{\, y : y>0 \,\}\)
\(y=\dfrac{1}{x}\) \(\{\, x : x\neq 0 \,\}\) \(\{\, y : y \neq 0 \,\}\)
\(y=\log_2 x\) \(\{\, x : x>0 \,\}\) \(\mathbb{R}\)

Interval notation

In geometry, an interval is the set of all points between two points \(A\) and \(B\) on a line.

Line with points A and B marked.

Sometimes the interval includes \(A\) and \(B\), in which case it is called closed. If it contains neither \(A\) nor \(B\), we call it an open interval.

In much of mathematics — particularly in calculus — we consider real functions, where both the domain of the function and the range of the function are subsets of the reals. Consequently, domains and ranges are very often intervals or unions of disjoint intervals.

Consider the sets \(A\) and \(B\) given by \[ A = \{\, x : 3\leq x\leq 5 \,\} \qquad\text{and}\qquad B = \{\, t : 3\leq t\leq 5 \,\}. \] Clearly \(A=B\), and the variables \(x\) and \(t\) are irrelevant! For this reason (and others), we use the notation \([3,5]\) to represent the set of all real numbers between 3 and 5, including 3 and 5. So \[ A = B = [3,5]. \] We call \([3,5]\) a closed interval, since it includes the endpoints. We use parentheses to denote an open interval, not including the endpoints, so \[ (3,5) = \{\, x : 3<x<5 \,\}. \] There are also half-open intervals \((3,5]\) and \([3,5)\). We use the symbols \(\infty\) and \(-\infty\) to define unbounded intervals: \begin{alignat*}{2} (3,\infty) &= \{\, x : x>3 \,\} &\qquad&\text{(open interval)} \\ (-\infty,3] &= \{\, x : x\leq 3 \,\} &&\text{(closed interval).} \end{alignat*} Note that \((-\infty,3] \cup (3,\infty) = \mathbb{R}\).

To summarise, let \(a,b\in\mathbb{R}\) with \(a<b\). In the following diagrams, a solid dot means that the point is included and an open dot that the point is not included.

Diagram showing all combinations of open and closed intervals.
Detailed description

Of course, the intervals \([a,\infty)\), \((a,\infty)\), \((-\infty,b]\) and \((-\infty,b)\) could also have been included. Notice that \[ (-\infty,a) \cup [a,b] \cup (b,\infty) = \mathbb{R}, \] as a disjoint union. Similarly, we have \[ (-\infty,a] \cup (a,b) \cup [b,\infty) = \mathbb{R}. \]

We will often use interval notation to describe domains. For example, the domain of \(y=\log_2 x\) is \((0,\infty)\), and the domain of \(y=\sqrt{x}\) is \([0,\infty)\).

Sometimes it is more convenient not to use intervals. For example, the domain of the function

\[ y = \dfrac{x-1}{(x-2)(x-3)}, \quad\text{for } x\notin \{2,3\}, \] is written most simply as \(\mathbb{R} \setminus \{2,3\}\). (A quotient of two polynomials is called a rational function.)

Next page - Content - Function notation