Assumed knowledge

• Familiarity with elementary set theory, as discussed in the TIMES module Sets and Venn diagrams (Years 7–8).
• Familiarity with the algebraic techniques described in the TIMES module Formulas (Years 9–10).
• The content of the modules Algebra review and Coordinate geometry.
• Basic knowledge of the modules Trigonometric functions and circular measure and Exponential and logarithmic functions.

Motivation

The expression \(y=x^2\), which links the two pronumerals \(x\) and \(y\), can be thought of in several different ways.

In the early years of school, we seek pairs of values, such as \((x,y) =(3,9)\), which satisfy the equation. These ordered pairs determine a graph. In this case, the graph is the standard parabola.

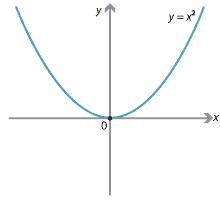
A formula is an equation relating different quantities using algebra. So \(y=x^2\) is also a formula. In fact, \(y=x^2\) is an example of a function, in the sense that each value of \(x\) uniquely determines a value of \(y\).

In this module, we will study the concept of a function. The formula \(A=\pi r^2\) gives \(A\) as a function of \(r\). The formula \(V=\pi r^2h\) expresses \(V\) as a function of the two variables \(r\) and \(h\). In this module, we will only consider functions of one variable, such as the polynomial

\[ y = (x-1)(x-2)(x-3)(x-4). \]

A clear understanding of the concept of a function and a familiarity with function notation are important for the study of calculus. The use of functions and function notation in calculus can be seen in the module Introduction to differential calculus.

Next page - Content - Set theory