Answers to exercises

Exercise 1

a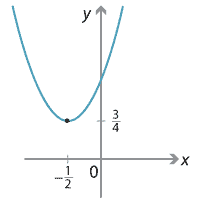 b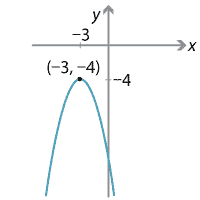

Detailed description of diagram

Exercise 2

The arms of the parabola \(y=x^2\) are steeper.

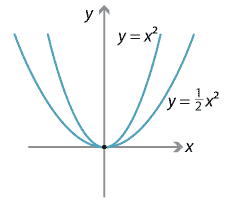
Detailed description of diagram

Exercise 3

\(y=2(x-1)^2+3\)

Exercise 4

The discriminant is \(36k^2-16(4k+1)\) and we set this equal to zero in order to obtain one real solution to the given equation. This gives \(9k^2-16k-4=0\), which has solutions \(k=2\) or \(k= -\dfrac{2}{9}\).

Exercise 5

The discriminant is \(\Delta = 36k^2\). One real solution occurs when \(\Delta=0\), which is when \(k=0\). The quadratic is never negative definite, since \(\Delta \geq 0\) for all values of \(k\).

Exercise 6

Divide the wire into \(4x\)cm for the circle and \((20-4x)\)cm for the square. (The 4 is to make the algebra easier.) The total area is then

\[ S=\dfrac{4x^2}{\pi} + (5-x)^2. \]

Since the leading coefficient is positive, the parabola has a minimum. We set \(\dfrac{dS}{dx}=0\) to find the stationary point, which occurs when \(x= \dfrac{5\pi}{4+\pi}\). Hence, we use \(\dfrac{20\pi}{4+\pi}\)cm for the circle and \(\dfrac{80}{4+\pi}\)cm for the square.

Exercise 7

\(x^2-4x-41\)

Exercise 8

• a \(\dfrac{4}{7}\)
• b \(-\dfrac{12}{49}\)

Exercise 9

We have

\begin{align*} (\alpha-\beta)^2 &= (\alpha+\beta)^2 - 4\alpha\beta\\ &= \Big({-}\dfrac{b}{a}\Big)^2 - \dfrac{4c}{a} = \dfrac{b^2-4ac}{a^2}. \end{align*}

Note that, if \(a=1\), then \((\alpha-\beta)^2\) is the discriminant of the quadratic. Similarly, we can define the discriminant of a monic cubic with roots \(\alpha, \beta, \gamma\) to be \((\alpha-\beta)^2(\alpha-\gamma)^2(\beta-\gamma)^2\), and so on for higher degree equations.

Exercise 10

The arithmetic mean is \(\dfrac{17}{6}\) and the geometric mean is 2. (Note that the actual roots are \(\dfrac{17\pm \sqrt{145}}{6}\) !)

Exercise 11

Successively substitute \(x=1\), \(x=2\), \(x=3\) and solve the resulting equations for \(a,b,c\) to obtain \(x^2=3(x-1)^2-3(x-2)^2+(x-3)^2\).

Exercise 12

Substituting the line into the circle we obtain \(x^2-4x+4=0\). The discriminant of this quadratic is 0 and so the line is tangent to the circle at \((2,1)\).

Exercise 13

The parabola can be written as \((y - 1)^2 = 4(x - 1)\). So the vertex is \((1,1)\), the focal length is \(a=1\), the focus is \((2,1)\), and the \(y\)-axis is the directrix.

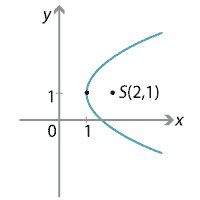
Detailed description of diagram

Exercise 14

The line \(3x+2y=1\).

Exercise 15

If \(PQ\) is a focal chord, then \(pq=-1\). Hence we can write the coordinates of \(Q\) as \(\big({-}\dfrac{2a}{p}, \dfrac{a}{p^2}\big)\). Thus

\begin{align*} PQ^2 &= \Big(2ap + \dfrac{2a}{p}\Big)^2 + \Big(ap^2 - \dfrac{a}{p^2}\Big)^2\\ &= 4a^2p^2 + 8a^2 + \dfrac{4a^2}{p^2} + a^2p^4 - 2a^2 + \dfrac{a^2}{p^4}\\ &= a^2\Big(p^4 + 4p^2 + 6 + \dfrac{4}{p^2} + \dfrac{1}{p^4}\Big)\\ &= a^2\Big(p + \dfrac{1}{p}\Big)^4, \end{align*}

where we recall the numbers \(1,4,6,4,1\) from Pascal's triangle and the binomial theorem. So \(PQ = a\Big(p+\dfrac{1}{p}\Big)^2\).

Exercise 16

The equations of the normals at \(P\) and \(Q\) are respectively

\[ x+py = 2ap+ap^3 \qquad \text{and} \qquad x+qy = 2aq+aq^3. \]

Subtracting we have

\[ y(p-q) = a(p^3-q^3)+2a(p-q) = a(p-q)(p^2+q^2+pq+2) \]

so \(y=a(p^2+q^2+pq+2)\). Substituting back we have \(x=-apq(p+q)\) after simplifying. Hence \(R\) is the point \(\big({-}apq(p+q), a(p^2+q^2+pq+2)\big)\).

Now, if \(PQ\) is a focal chord, then \(pq=-1\). Thus the \(x\)- and \(y\)-coordinates of \(R\) become \(x=a(p+q)\) and \(y = a(p^2+q^2+1) = a\big((p+q)^2+3\big)\), since \(pq=-1\). We can then eliminate \(p\) and \(q\) to obtain

\[ y=a\Bigg(\Big(\dfrac{x}{a}\Big)^2 + 3\Bigg) = \dfrac{x^2}{a} + 3a, \]

which is a parabola.

Exercise 17

Squaring

\[ \sqrt{(x-c)^2+y^2}= 2a - \sqrt{(x+c)^2+y^2}, \]

we have

\[ a\sqrt{(x+c)^2+y^2} = a^2+xc. \]

Squaring again and rearranging, we arrive at

\[ x^2(a^2-c^2) + a^2y^2= a^2(a^2-c^2). \]

Dividing by \(a^2(a^2-c^2)\) gives the desired equation.