Links forward

Conic sections

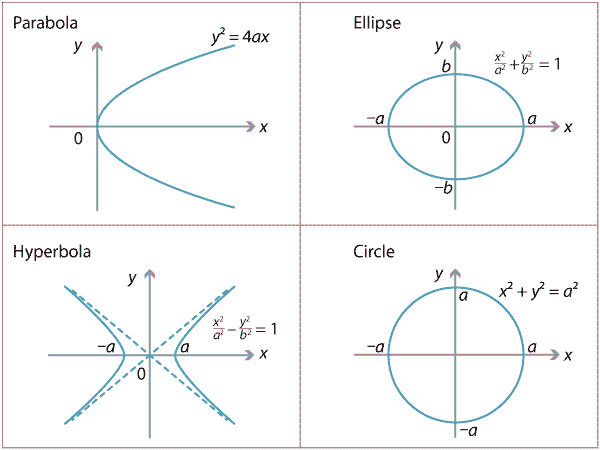
The parabola is one of the curves known as the conic sections, which are obtained when a plane intersects with a double cone.

The non-degenerate conic sections are the parabola, ellipse, hyperbola and circle.

4 diagrams of parabloa, ellipse, hyperbola and circle.
Detailed description of diagram

The degenerate case produces also a line, a pair of lines and a point.

Locus definitions

The ellipse and hyperbola can be defined as a locus in various ways.

Suppose we fix two distinct points \(F_1\) and \(F_2\) in the plane. Then the ellipse can be defined as the locus of points \(P\) such that the sum of the distances \(PF_1 + PF_2\) is a fixed constant \(2a\). (Imagine pinning down the ends of a piece of string at the points \(F_1\) and \(F_2\), then using a pencil to pull the string tight and allowing the pencil to move around the page. The sum of the distances is then the length of the string, which remains constant.)

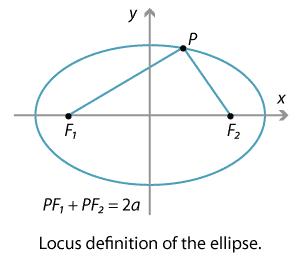
Locus definition of the ellipse.
Detailed description of diagram

Thus, if we set the points to be \(F_1(-c,0)\) and \(F_2(c,0)\), with \(0 < c < a\), then the sum of the distances is

\[ \sqrt{(x-c)^2+y^2} + \sqrt{(x+c)^2+y^2} = 2a. \]

Taking the second square root onto the other side, squaring, simplifying and squaring again, we obtain the equation

\[ \dfrac{x^2}{a^2} + \dfrac{y^2}{a^2-c^2} = 1. \]

If we write \(b^2=a^2-c^2\), then the equation becomes

\[ \dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1. \]

This is the cartesian equation of the ellipse.

Exercise 17

Perform the algebra suggested above to derive the equation of the ellipse.

If, instead, we require the difference of the distances \(PF_1 - PF_2\) to be a fixed constant \(2a\), then we obtain part of a hyperbola. The equation has the form \(\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\).

2 grpahs. 1. PF one – PF two= 2a. Line segments PF one and PF two drawn. F one and F two are on the x-axis. 2. Hyperbola drawn next to the first.
Detailed description of diagrams

Focus-directrix definitions

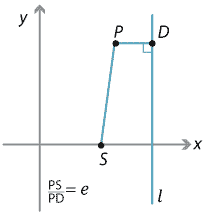
Recall that the parabola can be defined as the locus of the point \(P\) moving so that the distance \(PS\), from \(P\) to the focus \(S\), is equal to the perpendicular distance of \(P\) to the directrix \(l\). Thus, if \(D\) is the nearest point on \(l\) to \(P\), we have \({PS}={PD}\), which we can write as \(\dfrac{PS}{PD}=1\).

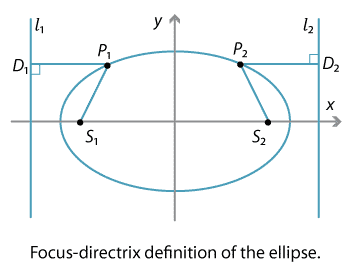
The ellipse and the hyperbola also have focus-directrix definitions as we can see in the diagram below.

PS over PD = e. Directrix line drawn parallel to y axis. Point S chosen as focus. Line segments PS and PD are drawn where PD is perpendicular to the directrix.
Detailed description of diagram

We choose a fixed point \(S\), which will be the focus, and a line \(l\) (not containing \(S\)). Take the locus of all points \(P\) such that, if \(D\) is the nearest point on \(l\) to \(P\), then the ratio of the distances \(\dfrac{PS}{PD}\) is equal to a fixed positive number \(e\), called the eccentricity.

If \(e\) is equal to 1, then we have, of course, the parabola. The name parabola comes from the Greek meaning 'fall beside' since, in the case of the parabola, the distance \(PS\) is equal to (i.e., falls beside) the distance \(PD\).
If \(e\) is less than 1, then we obtain an ellipse (from the Greek meaning 'fall short of' — the original sense was that \(PS\) falls short of \(PD\)).
If \(e\) is greater than 1, then we have a hyperbola (from the Greek meaning 'exceed' — the original sense was that \(PS\) exceeds \(PD\)).

Screencast of interactive 3 , Interactive 3

Ellipse, centre the origin. Two directrices L one and L two. Two Foci S one and S two.
Detailed description of diagram

As we saw above, the cartesian equation of the ellipse is

\[ \dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}=1. \]

It can be shown that the eccentricity \(e\) of the ellipse is connected to the quantities \(a\) and \(b\) by the equation \(b^2=a^2(1-e^2)\). The foci can be written as \((\pm ae, 0)\), while the equations of the directrices are \(x= \pm \dfrac{a}{e}\).

Similarly, for the hyperbola

\[ \dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}=1, \]

the eccentricity is connected to the quantities \(a\) and \(b\) by the equation \(b^2=a^2(e^2-1)\).

The ellipse also has a reflective property in that any light beam emanating from one of the two foci will reflect off the curve and pass through the other focus. This idea has been widely exploited in acoustics and optics.

Second-degree equations

Algebraically, every second-degree equation of the form \(Ax^2+By^2+Cxy+Dx+Ey =F\) can be shown, by means of linear changes of variables, to be similar to one of the conic sections (including the degenerate cases) we have listed above.

For example, the equation \(x^2+y^2-4x+6y=0\) can be written as \((x-2)^2+(y+3)^2 = 13\), which is a circle. Similarly, the equation \(x^2-y^2=0\) can be written as \((x-y)(x+y)=0\) and so as \(y=x\) or \(y=-x\), which is a pair of lines.

An equation such as \(x^2+y^2+6xy=1\) in fact represents a hyperbola, but one which is rotated about the origin. The theory of matrices is generally used to analyse such equations, but this is not part of secondary school mathematics.

Three-dimensional analogues

Each of these curves has a three-dimensional analogue. For example, the parabolic reflector is an example of a paraboloid. The basic paraboloid has equation \(z=x^2+y^2\) and its cross-section in the \(y\)–\(z\) plane is a parabola. Similarly, an ellipsoid has the basic shape of a football, with equation

\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2} =1. \]

In the case when \(a=b=c\), we have a sphere.

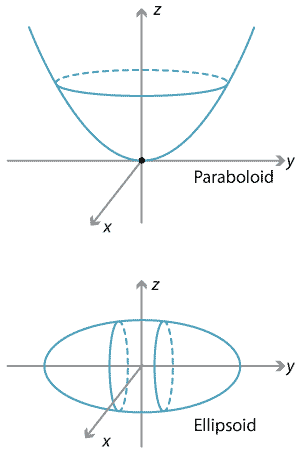
2 diagrams. 1. Illustration of a three dimensional Paraboloid.
2. Illustration of a three dimensional Ellipsoid.
Detailed description of diagrams

There are also 3-dimensional hyperboloids of one and two sheets.

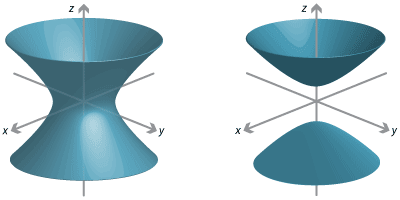
2 diagrams. 1. Illustration of a three dimensional hyperboloids with one sheet.
2. Illustration of a three dimensional hyperboloids with two sheets.
Detailed description of diagrams

Next page - History and applications