Content - Intersection of lines and parabolas

Intersection of lines and parabolas

In this section we investigate under what conditions a line and a parabola might meet in the plane. It is easy to see that there are three main cases to consider.

A line may:

intersect a parabola at two points
touch a parabola at one point (in this case we say the line is tangent to the parabola)
not intersect the parabola at all.

The three cases are shown in the diagrams below.

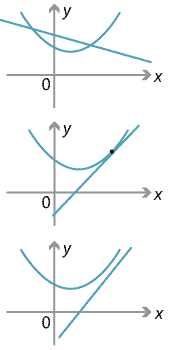
Three diagrams. One with line touching, one wit line crossing and one with line not meeting the parabola.
Detailed description of diagram

There is also a special case when the line is parallel to the \(y\)-axis. In this case the line will cut the parabola once. Having noted this case, we will not need to consider it further, since the intersection point is easily found.

Suppose the line has the form \(y=mx+d\) and the parabola is \(y=ax^2+bx+c\). Equating, we have

\[ ax^2+bx+c = mx+ d \ \implies \ ax^2+(b-m)x+(c-d)=0. \]

This gives a quadratic equation. Hence we can conclude:

A line can meet a parabola in at most two points.
If the discriminant of the resulting quadratic is negative, the line does not meet the parabola at all.
If the discriminant of the resulting quadratic is positive, the line meets the parabola in two distinct points.
If the discriminant of the resulting quadratic is zero, then the line is tangent to the parabola.

Example

Discuss the intersection of the line \(y=3x+2\) and the parabola \(y=4x^2-9x+11\).

Solution

Equating the two equations, we have

\[ 4x^2-9x+11 = 3x+2 \ \implies \ 4x^2-12x+9=0. \]

Now the discriminant of this quadratic is \(b^2-4ac = 144-4\times 4\times 9 = 0\) and so the equation has only one solution. Hence the line is tangent to the parabola.

Exercise 12

Use the ideas above to show that the line \(y=-2x+5\) is tangent to the circle
\(x^2+y^2=5\).

Screencast of exercise 12

Next page - Content - Focus-directrix definition of the parabola