Applications to maxima and minima

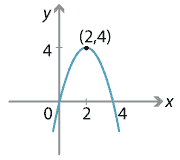
Since every parabola has a vertex, the \(y\)-coordinate of the vertex gives the maximum or minimum value of \(y\) for all possible values of \(x\).

For example, the vertex of the parabola \(y=4x-x^2\) is \((2,4)\) and the greatest \(y\)-value is 4.

y = 4x – x squared, parabola, turning point at (2,4), x intercepts at (0,0) and (4,0), y intercept at (0,0).
Detailed description of diagram

There are a number of geometric problems and word problems in which the variables are connected via a quadratic function. It is often of interest to maximise or minimise the dependent variable.

Example

A farmer wishes to build a large rectangular enclosure using an existing wall. She has 40 m of fencing wire and wishes to maximise the area of the enclosure. What dimensions should the enclosure have?

Solution

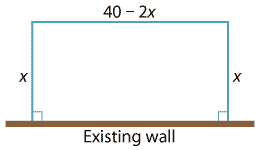
Rectangle, vertical sides marked as x, top of rectangle marked as 40-2x, bottom of rectangle marked as 'existing wall'.
Detailed description of diagram

With all dimensions in metres, let the width of the enclosure be \(x\). Then the three sides to be made from the fencing wire have lengths \(x\), \(x\) and \(40-2x\), as shown in the diagram.

Thus the area \(A\) is given by

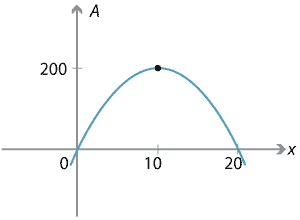
\[ A = x(40-2x) = 40x-2x^2. \]

This gives a quadratic relationship between the area and the width, which can be plotted.

A = x(40-2x) = 40x - 2x squared, parabola, y axis marked as A, turning point at (10,200), x intercepts at (0,0) and (20,0), y intercept at (0,0).
Detailed description of diagram

Clearly the area will be a maximum at the vertex of the parabola. Using \(x=-\dfrac{b}{2a}\), we see that the \(x\)-value of the vertex is \(x=10\).

Hence the dimensions of the rectangle with maximum area are 10 m by 20 m, and the maximum area of the enclosure is 200 m\(^2\).

Note. Differential calculus can be used to solve such problems. While this is quite acceptable, it is easier to use the procedure outlined above. You may use calculus, however, to solve the following exercise.

Exercise 6

A piece of wire with length 20cm is divided into two parts. One part is bent to form a circle while the other is bent to form a square. How should the wire be divided in order that the sum of the areas of the circle and square is minimal?

Next page - Content - Sum and product of the roots