Content - The quadratic formula and the discriminant

The quadratic formula and the discriminant

The quadratic formula was covered in the module Algebra review. This formula gives solutions to the general quadratic equation \(ax^2+bx+c=0\), when they exist, in terms of the coefficients \(a,b,c\). The solutions are

\[ x = \dfrac{-b+\sqrt{b^2-4ac}}{2a}, \qquad x = \dfrac{-b-\sqrt{b^2-4ac}}{2a}, \]

provided that \(b^2-4ac \geq 0\).

The quantity \(b^2-4ac\) is called the discriminant of the quadratic, often denoted by \(\Delta\), and should be found first whenever the formula is being applied. It discriminates between the types of solutions of the equation:

\(\Delta > 0 \) tells us the equation has two distinct real roots
\(\Delta = 0 \) tells us the equation has one (repeated) real root
\(\Delta < 0 \) tells us the equation has no real roots.

Screencast of interactive 2 , Interactive 2

Exercise 4

For what values of \(k\) does the equation \((4k+1)x^2-6kx+4=0\) have one real solution?

A quadratic expression which always takes positive values is called positive definite, while one which always takes negative values is called negative definite.

Quadratics of either type never take the value 0, and so their discriminant is negative. Furthermore, such a quadratic is positive definite if \(a > 0\), and negative definite if \(a < 0\).

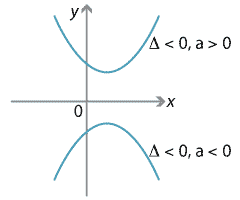
Two parabolas one entirely above the x axis and one entirely below.
Detailed description of diagram

Example

Show that the quadratic expression \(4x^2-8x+7\) always takes positive values for any value of \(x\).

Solution

In this case, \(a=4\), \(b=-8\) and \(c=7\). So

\[ \Delta = (-8)^2 - 4\times 4 \times 7 = -48 < 0 \]

and \(a=4 > 0\). Hence the quadratic is positive definite.

Exercise 5

For what values of \(k\) does the equation \((4k+1)x^2-2(k+1)x+(1-2k)=0\) have one real solution? For what values of \(k\), if any, is the quadratic negative definite?

Screencast of exercise 5

Next page - Content - Applications to maxima and minima