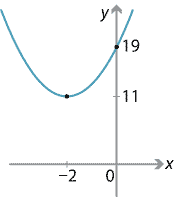The axis of symmetry
All parabolas have exactly one axis of symmetry (unlike a circle, which has infinitely many axes of symmetry). If the vertex of a parabola is \((k,l)\), then its axis of symmetry has equation \(x=k\).
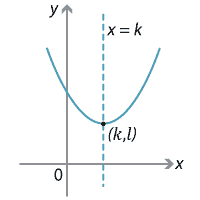
Detailed description of diagram
We can find a simple formula for the value of \(k\) in terms of the coefficients of the quadratic. As usual, we complete the square:
\begin{align*} y &= ax^2 + bx + c\\ &= a\Big[x^2 + \dfrac{b}{a}x + \dfrac{c}{a}\Big]\\ &= a\Big[\Big(x+\dfrac{b}{2a}\Big)^2 + \dfrac{c}{a} - \Big(\dfrac{b}{2a}\Big)^2\Big]. \end{align*}We can now see that the \(x\)-coordinate of the vertex is \(-\dfrac{b}{2a}\). Thus the equation of the axis of symmetry is
\[ x = -\dfrac{b}{2a}. \]We could also find a formula for the \(y\)-coordinate of the vertex, but it is easier simply to substitute the \(x\)-coordinate of the vertex into the original equation \(y=ax^2+bx+c\).
Example
Sketch the parabola \(y=2x^2+8x+19\) by finding the vertex and the \(y\)-intercept. Also state the equation of the axis of symmetry. Does the parabola have any \(x\)-intercepts?
Solution
Here \(a=2\), \(b=8\) and \(c=19\). So the axis of symmetry has equation \(x=-\dfrac{b}{2a}=-\dfrac{8}{4}=-2\). We substitute \(x=-2\) into the equation to find \(y = 2\times (-2)^2 + 8\times (-2) + 19 = 11\), and so the vertex is at \((-2,11)\). Finally, putting \(x=0\) we see that the \(y\)-intercept is 19.
There are no \(x\)-intercepts.
Exercise 3
A parabola has vertex at \((1,3)\) and passes through the point \((3,11)\). Find its equation.
Next page - Content - The quadratic formula and the discriminant
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |