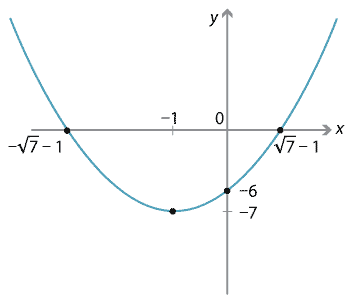Intercepts
Thus far we have concentrated on the transformational aspects of the graphs of quadratics and the coordinates of the vertex. Of course one may also be interested in the points at which the graph crosses the \(x\)- and \(y\)-axes. These are called the intercepts. It is easy to find the \(y\)-intercept of a parabola — it always has one — by putting \(x=0\). Not all parabolas, however, have \(x\)-intercepts. When \(x\)-intercepts exist, they are obtained by putting \(y=0\) and solving the resulting quadratic equation.
As we know, there are many ways to solve a quadratic equation, and there are obvious choices of strategy depending on the given problem. If we have already completed the square to find the vertex, then we can use that to quickly find the \(x\)-intercepts.
Example
Find the vertex and intercepts of \(y=x^2+2x-6\) and sketch the parabola.
Solution
Completing the square gives \(y=(x+1)^2-7\), so the vertex is at \((-1,-7)\).
Putting \(x=0\), we find that the \(y\)-intercept is \(-6\). Putting \(y=0\) to find the
\(x\)-intercepts, we have \((x+1)^2-7=0\) and so \((x+1)^2=7\), which gives \(x=-1+\sqrt{7}\), \(x=-1-\sqrt{7}\).
Completing the square will also tell us when there are no \(x\)-intercepts. For example, given the quadratic \(y=x^2+6x+13\), completing the square yields \(y=(x+3)^2+4\). We can see that \(y\) is never zero, since the right-hand side is at least 4 for any value of\(x\).
In some instances — especially when completing the square is harder — we may prefer to use the factor method instead. For example, the quadratic \(y=x^2-5x+6\) factors to \({y=(x-3)(x-2)}\), and so we can easily see that the \(x\)-intercepts are at \(x=2\) and \(x=3\).
There are a number of strategies to find the vertex. You will have seen in the examples that, since the graph of the quadratic function is symmetric about the vertex, the \(x\)-intercepts are symmetric about the vertex. Hence the average of the \(x\)-intercepts gives the \(x\)-coordinate of the vertex. This is very useful in those situations in which we have already found the \(x\)-intercepts.
For example, the quadratic function \(y= x^2-5x+6\) has its \(x\)-intercepts at \(x=2\) and \(x=3\). Hence the \(x\)-coordinate of the vertex is the average of these numbers, which is \(2\dfrac{1}{2}\). From this we can find the \(y\)-coordinate of the vertex, which is \(-\dfrac{1}{4}\).
Of course, not all parabolas have \(x\)-intercepts. In the next section, we give a formula for the \(x\)-coordinate of the vertex of \(y=ax^2+bx+c\).