The reflection property of the parabola

While the parabola has many beautiful geometric properties as we have seen, it also has a remarkable property known as the reflection property, which is used in such diverse places as car headlights and satellite dishes. A car headlight emits light from one source, but is able to focus that light into a beam so that the light does not move off in all directions — as lamplight does — but is focused directly ahead. Satellite dishes do the opposite. They collect electromagnetic rays as they arrive and concentrate them at one point, thereby obtaining a strong signal.

Headlight reflectors and satellite dishes are designed so their cross-sections are parabolic in shape and the point of collection or emission is the focus of the parabola.

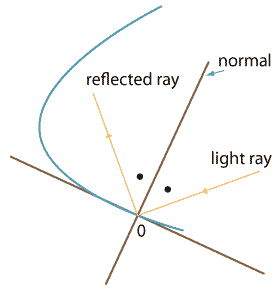
To show how this works we need a basic fact from physics: when light (or any electromagnetic radiation) is reflected off a surface, the angle of incidence equals the angle of reflection. That is, when a light ray bounces off the surface of a reflector, then the angle between the light ray and the normal to the reflector at the point of contact equals the angle between the normal and the reflected ray. This is shown in the following diagram.

No equation given, parabola showing that a light ray and the reflection of that light ray form equal angles with the normal to the parabola at the point of incidence.
Detailed description of diagram

Note that this implies that the angle between the ray and the tangent is also preserved after reflection, which is a more convenient idea for us here.

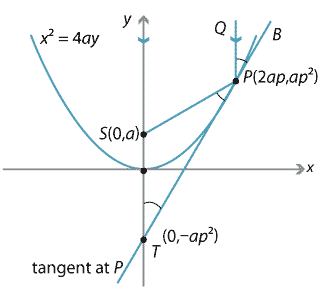
Let \(P(2ap,ap^2)\) be a point on the parabola \(x^2=4ay\) with focus at \(S\) and let \(T\) be the point where the tangent at \(P\) cuts the \(y\)-axis.

Suppose \(PQ\) is a ray parallel to the \(y\)-axis. Our aim is to show that the line \(PS\) will satisfy the reflection property, that is, \(\angle QPB\) is equal to \(\angle SPT\).

x squared = 4ay, parabola, turning point at (0, 0). Tangent at a point P(2ap,ap squared) drawn. the focus S(0, a).
Detailed description of diagram

Notice that, since \(QP\) is parallel to \(ST\), \(\angle QPB\) is equal to \(\angle STP\), so we will show that \(\angle STP = \angle SPT\).

Now \(S\) has coordinates \((0,a)\), and \(T\) has coordinates \((0,-ap^2)\), obtained by putting \(x=0\) in the equation of the tangent at \(P\). Hence

\[ SP^2=(2ap-0)^2+(ap^2-a)^2 = a^2(p^2+1)^2 \] after a little algebra. Also, \[ ST^2 = (a+ap^2)^2= a^2(1+p^2)^2 \]

and so \(SP=ST\). Hence \(\Delta STP\) is isosceles and so \(\angle STP = \angle SPT\).

Illustration of parabola with light rays parallel to the axis of symmetry being reflected through the focus.

Detailed description of diagram

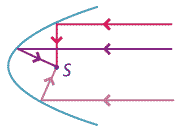
Thus the reflection property tells us that any ray parallel to the axis of the parabola will bounce off the parabola and pass through the focus. Conversely, any ray passing through the focus will reflect off the parabola in a line parallel to the axis of the parabola (so that light emanating from the focus will reflect in a straight line parallel to the axis).



Next page - Links forward - Conic sections