Chords, tangents and normals
Chords
Again, we consider the parabola \(x^2=4ay\), for some \(a > 0\), and the parametrisation
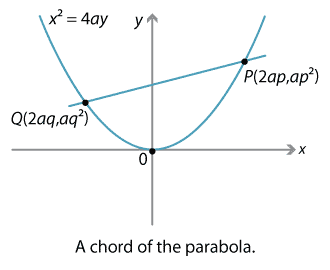
\begin{align*} x &= 2at\\ y &= at^2. \end{align*}When we take two distinct points \(P,Q\) on the parabola, we can join them to form a line segment called a chord. Sometimes we will refer to the line through \(P\) and \(Q\) as the chord.
Let the value of the parameter \(t\) at the points \(P\) and \(Q\) be \(p\) and \(q\) respectively. Thus \(P\) has coordinates \((2ap, ap^2)\) and \(Q\) has coordinates \((2aq, aq^2)\).
Detailed description of diagram
The gradient of the line \(PQ\) is given by
\[ \dfrac{ap^2-aq^2}{2ap-2aq} = \dfrac{a(p^2-q^2)}{2a(p-q)}= \dfrac{p+q}{2}. \]So the gradient of the chord is the average of the values of the parameter. (One of the many reasons this parametrisation was chosen.)
Hence the equation of the chord is
\[ y-ap^2 = \dfrac{p+q}{2}(x-2ap), \]which rearranges to
\[ y = \dfrac{p+q}{2}x-apq. \]It is best to reconstruct this equation each time rather than memorise it.
A chord which passes through the focus of a parabola is called a focal chord. A given chord will be a focal chord if the point \((0,a)\) lies on it. Substituting these coordinates into the equation of the chord above we have
\[ a= \dfrac{p+q}{2}\times 0 -apq, \]which is equivalent to \(pq=-1\). This gives us a simple condition to tell when the chord joining two points is a focal chord.
Thus \(PQ\) is a focal chord if and only if \(pq=-1\). The basic fact should be committed to memory.
Example
Suppose \(P(2ap, ap^2)\) and \(Q(2aq,aq^2)\) are two points lying on the parabola \(x^2=4ay\).
Prove that, if \(OP\) and \(OQ\) are perpendicular, then \(pq=-4\).
Solution
The gradient of \(OP\) is \(\dfrac{ap^2}{2ap}= \dfrac{p}{2}\) and similarly the gradient of \(OQ\) is \(\dfrac{q}{2}\). Since these lines are perpendicular, the product of their gradients is \(-1\) and so \(\dfrac{p}{2}\times\dfrac{q}{2}=-1\), which implies that \(pq= -4\).
Note that, in this case, \(PQ\) can never be a focal chord.
Exercise 15
Suppose \(P(2ap, ap^2)\) and \(Q(2aq,aq^2)\) are two points lying on the parabola \(x^2=4ay\). Prove that, if \(PQ\) is a focal chord, then the length of the chord \(PQ\) is given by \( a\big(p+\dfrac{1}{p}\big)^2\).
Tangents
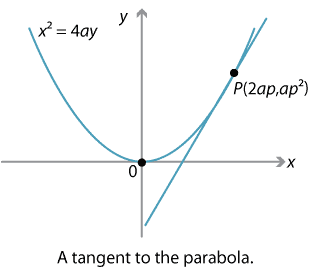
We have seen that the gradient of the chord joining two distinct points \(P(2ap,ap^2)\) and \(Q(2aq,aq^2)\) on the parabola \(x^2=4ay\) is \(\dfrac{1}{2}(p+q)\).
If we now imagine the point \(Q\) moving along the parabola to the point \(P\), then the line through \(P\) and \(Q\) will become a tangent to the parabola at the point \(P\). Putting \(q=p\), we see that the gradient of this tangent is \(\dfrac{1}{2}(p+p) = p\).
Detailed description of diagram
We could also find the gradient of the tangent by differentiating
\[ y= \dfrac{x^2}{4a} \]and substituting \(x=2ap\). In either case, the gradient of the tangent to \(x^2=4ay\) at the point \(P(2ap,ap^2)\) is \(p\). (This is the main reason for this choice of parametrisation.)
Hence the equation of the tangent to the parabola at \(P\) is given by
\[ y-ap^2= p(x-2ap) \ \implies \ y=px-ap^2. \]This formula is best derived each time it is needed rather than memorised.
Normals
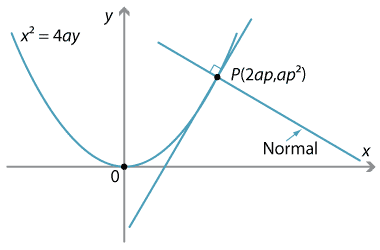
The line through a point \(P\) perpendicular to the tangent to the curve at \(P\) is called the normal to the curve at \(P\).
Since the normal and tangent are perpendicular, the product of their gradients is \(-1\) and so the gradient of the normal at \(P(2ap, ap^2)\) is \(-\dfrac{1}{p}\). Hence the equation of the normal at \(P\) is
\[ y-ap^2 = -\dfrac{1}{p}(x-2ap) \ \implies \ x+py = 2ap+ap^3. \]Once again, this is best derived each time rather than memorised.
Detailed description of diagram
Example
Find the point of intersection of the tangents to the parabola \(x^2=4ay\) at the points \(P(2ap,ap^2)\) and \(Q(2aq,aq^2)\). What can be said about this intersection point if the chord \(PQ\) is a focal chord?
Solution
The equations of the tangents at \(P\) and \(Q\) are respectively \(y=px-ap^2\) and \(y=qx-aq^2\). Equating these we find
\[ px-ap^2=qx-aq^2 \ \implies \ x= a(p+q). \]Substituting back we find that the \(y\)-coordinate is \(y=apq\) and so the point of intersection is \(\big(a(p+q), apq\big)\).
Now, if \(PQ\) is a focal chord, then \(pq=-1\) and so the point of intersection becomes \({\big(a(p-\dfrac{1}{p}), -a\big)}\). While the \(x\)-coordinate of this point can vary, the \(y\)-coordinate is always \(-a\) and so the point of intersection always lies on the directrix.
Exercise 16
Find the point of intersection \(R\) of the normals to the parabola \(x^2=4ay\) at the points \(P(2ap, ap^2)\) and \(Q(2aq, aq^2)\).
Show that, if \(PQ\) is a focal chord, then the point \(R\) always lies on a certain parabola, and find the equation of this parabola.
Next page - Content - The reflection property of the parabola
