Parametric equations of a parabola
Since every parabola is congruent to \(x^2=4ay\), for some choice of \(a > 0\), we can study the geometry of every parabola by confining ourselves to this one! This shows the power of both coordinate geometry and transformations.
Imagine a particle moving in the plane along a curve \(C\) as shown.
Detailed description of diagram
The \(x\)- and \(y\)-coordinates of the particle can be thought of as functions of a new variable \(t\), and so we can write \(x=f(t)\), \(y=g(t)\), where \(f,g\) are functions of \(t\). In some physical problems \(t\) is thought of as time.
The equations
\begin{align*} x &= f(t)\\ y &= g(t) \end{align*}are called the parametric equations of the point \(P(x,y)\) and the variable \(t\) is called a parameter.
It is often very useful to take a cartesian equation \(y=F(x)\) and introduce a parameter \(t\) so that the \(x\)- and \(y\)-coordinates of any point on the curve can be expressed in terms of this parameter.
Here is a very simple example of a parametrisation. Suppose we begin with the line whose equation is \(y=3x-4\). We can introduce a new variable \(t\) and write \(x=t\). Then we have \(y=3t-4\). Thus we can rewrite the equation \(y=3x-4\) in parametric form as
\begin{align*} x &= t\\ y &= 3t-4. \end{align*}Exercise 14
Eliminate the parameter \(t\) from the equations
\begin{align*} x &= 2t-3\\ y &= 5-3t \end{align*}and describe the resulting function.
Another common parametrisation is that used for a circle. The cartesian equation of a circle of radius \(r\) centred at the origin is \(x^2+y^2 = r^2\). We can put \(x = r\cos\theta\), \(y = r\sin\theta\), and we see that
\[ x^2+y^2 = r^2\cos^2\theta + r^2\sin^2\theta = r^2(\cos^2\theta + \sin^2\theta) = r^2, \]so these satisfy the original equation. The angle \(\theta\) here is the parameter and measures the angle between the positive \(x\)-axis and a radial line to the circle.
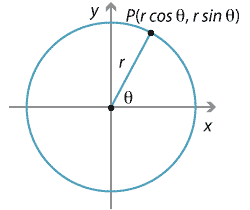
Detailed description of diagram
Thus we can describe the circle parametrically by
\begin{align*} x &= r\cos\theta\\ y &= r\sin\theta, \end{align*}where \(0\leq \theta < 2\pi\).
The parabola \(x^2=4ay\), where \(a > 0\), may also be parametrised and there are many ways to do this. We will choose the parametrisation
\begin{align*} x &= 2at\\ y &= at^2. \end{align*}The parameter in this case is \(t\).
This is the standard parametrisation for the parabola \(x^2=4ay\) and the reason for this parametrisation will become apparent later in this module.
You should check that this parametrisation actually satisfies the original equation.
Example
Express the parabola \(x^2= 12y\) parametrically.
Solution
In this case we see that \(a=3\) and so the general point on the parabola can be expressed parametrically as
\begin{align*} x &= 6t\\ y &= 3t^2. \end{align*}