Focus-directrix definition of the parabola

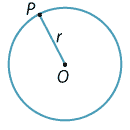
The Greeks defined the parabola using the notion of a locus. A locus is a set of points satisfying a given condition. These points will generally lie on some curve. For example, the circle with centre \(O\) and radius \(r\) is the locus of a point \(P\) moving so that its distance from the point \(O\) is always equal to \(r\).

Circle, centre marked as 0, point on circumference of circle marked as P, straight line connecting point at perimeter to centre marked as r.
Detailed description of diagram

The locus definition of the parabola is only slightly more complicated. It is very important and gives us a new way of viewing the parabola. One of the many applications of this is the refection principle, which we will look at in a later section.

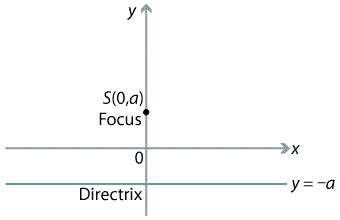
We fix a point in the plane, which we will call the focus, and we fix a line (not through the focus), which we will call the directrix. It is easiest to take the directrix parallel to the \(x\)-axis and choose the origin so that it is equidistant from the focus and directrix. Thus, we will take the focus at \(S(0,a)\) and the directrix with equation \(y=-a\), where \(a > 0\). This is as shown in the following diagram.

Line y = -a, where a > 0. The point which is the focus marked as S(0,a), directrix is the line y=-a.
Detailed description of diagram

We now look at the locus of a point moving so that its distance from the focus is equal to its perpendicular distance to the directrix. Let \(P(x,y)\) be a point on the locus. Our aim is to find the equation governing the coordinates \(x\) and \(y\) of \(P\).

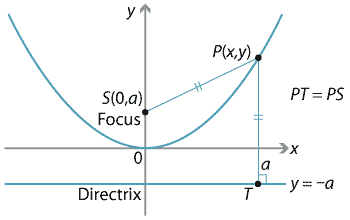
No equation given, parabola with turning point at (0,0), point marked on parabola in quadrant 1 as P(x,y), focus marked as S(0,a), directrix labelled as y = −a,.
Detailed description of diagram

The distance \(PS\) is equal to \(\sqrt{x^2 + (y-a)^2}\), and we can see from the diagram that the perpendicular distance \(PT\) of \(P\) to the directrix is simply \(y+a\).

Since \(PS=PT\), we can square each length and equate, giving

\[ x^2+(y-a)^2 = (y+a)^2 \ \implies \ x^2=4ay. \]

The last equation may also be written as

\[ y= \dfrac{x^2}{4a} \]

and so we see that it is the equation of a parabola with vertex at the origin.

The positive number \(a\) is called the focal length of the parabola.

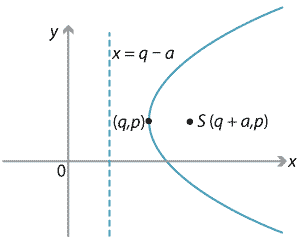
Any parabola of the form \(y=Ax^2+Bx+C\) can be put into the standard form

\[ (x-p)^2 = \pm 4a(y-q), \]

with \(a > 0\), where \((p,q)\) is the vertex and \(a\) is the focal length. When a parabola is in this standard form, we can easily read off its vertex, focus and directrix.

Example

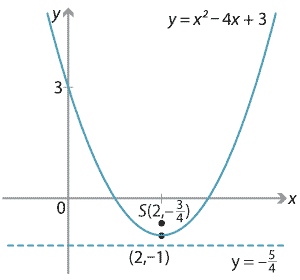
Find the vertex, focal length, focus and directrix for the parabola \(y=x^2-4x+3\).

Solution

We complete the square and rearrange as follows:

\begin{align*} y = x^2-4x+3 \ &\implies \ y=(x-2)^2-1 \\ \ &\implies \ (x-2)^2= 4\times \dfrac{1}{4}(y+1). \end{align*}

Hence the vertex is \((2,-1)\) and the focal length is \(\dfrac{1}{4}\).

The focus is then \((2, -\dfrac{3}{4})\) and the equation of the directrix is \(y=-\dfrac{5}{4}\).

Parabola, turning point at (2, minus1), intercepts y axis at (0,3), two x intercepts, directrix labelled as y = minus 5 over 4, focus labelled as S(2, minus 3 over 4).
Detailed description of diagram

A parabola may also have its directrix parallel to the \(y\)-axis and then the standard form is \((y-p)^2 = \pm 4a(x-q)\), with \(a > 0\).

(y - p)squared = plus or minus 4a(x - q), with a > 0, Parabola with x axis as axis of symmetry, vertex marked as (q, p), intercepts positive x axis.
Detailed description of diagram

Exercise 13

Put the parabola \(y^2-2y= 4x-5\) into the above standard form (for a directrix parallel to the \(y\)-axis) and thus find its vertex, focus and directrix, and sketch its graph.

Next page - Content - Parametric equations of a parabola