History and applications

The Greeks

The ancient Greek mathematicians were very interested in ratios. Indeed, much of their arithmetic was done geometrically using lengths and ratios. They found the link between ratios and music — hence the origin of the term harmonic mean.

The Greeks defined several different means. Less well known is the Heronian mean \(N(a,b)\) of two positive real numbers \(a\) and \(b\), which is the average of the three numbers \(a\), \(b\) and their geometric mean. That is,

\[ N(a,b) = \dfrac{a + b + \sqrt{ab}}{3}. \]

Notice that, for \(a,b>0\), we have

\[ \dfrac{a + b + \sqrt{ab}}{3} \geq \dfrac{2\sqrt{ab} + \sqrt{ab}}{3} = \sqrt{ab} \] and \[ \dfrac{a + b + \sqrt{ab}}{3} \leq \dfrac{a + b + \dfrac{a+b}{2}}{3} = \dfrac{a+b}{2}, \]

giving

\[ \sqrt{ab} \leq N(a,b) \leq \dfrac{a+b}{2}. \]

That is, the Heronian mean lies in between the geometric and arithmetic means.

Again, we can generalise and define the Heronian mean \(N\) of \(n\) positive real numbers \(a_1,a_2,\dots,a_n\) to be

\[ N = \dfrac{a_1 + a_2 + \dots + a_n + \sqrt[n]{a_1a_2\dots a_n}}{n+1}. \]

The Greeks were also interested in various types of sequences and series. They of course knew the sequence of square numbers

\[ 1,\ 4,\ 9,\ 16,\ \dots \]

but they also introduced the sequence of triangular numbers

\[ 1,\ 3,\ 6,\ 10,\ \dots \]

given by \(T_1 = 1\) and \(T_n = T_{n-1} + n\), for \(n \geq 2\). The general term of this sequence is

\[ T_n = 1 + 2 + \dots + n = \dfrac{1}{2}n(n+1). \]

These numbers may be represented graphically, as follows.

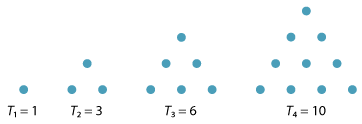
Detailed description
The first four triangular numbers.

The Greeks used geometric techniques to show that

\[ 1^2 + 2^2 + 3^2 + \dots + n^2 = \dfrac{1}{6}n(n+1)(2n+1) \] and \[ 1^3 + 2^3 + 3^3 + \dots + n^3 = \dfrac{1}{4}n^2(n+1)^2 = (1 + 2 + 3 + \dots + n)^2. \]

Next page - Answers to exercises