Links forward

Connection with integration

Integration is used to find the area under a curve. We can approximate the area under the curve by rectangles, and add up the areas of the rectangles. This gives a finite series. By taking more rectangles of smaller width, we obtain a series that better approximates the area. We can define the area under the curve to be the limit of the sequence of sums, provided the limit exists.

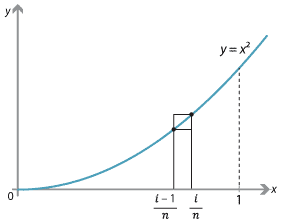
Consider, for example, the function \(f(x)=x^2\) on the interval \([0,1]\). We will look at the region \(R\) bounded by the curve, the \(x\)-axis and the line \(x=1\).

Detailed description
Approximating the area under \(f(x)=x^2\) on the interval \([0,1]\).

Divide the interval \([0,1]\) into \(n\) equal subintervals of width \(\dfrac{1}{n}\). For \(i=1,2,\dots,n\), we construct two rectangles \(U_i\) and \(L_i\) on the subinterval \(\bigl[\dfrac{i-1}{n}, \dfrac{i}{n}\bigr]\), where

• the height of \(U_i\) is the maximum value of \(f(x)\) on the subinterval, namely \(\bigl(\dfrac{i}{n}\bigr)^2\)
• the height of \(L_i\) is the minimum value of \(f(x)\) on the subinterval, namely \(\bigl(\dfrac{i-1}{n}\bigr)^2\).

We can obtain an upper bound for the area of \(R\) by finding the total area \(A_n\) of the \(n\) rectangles \(U_1,U_2,\dots,U_n\):

\begin{alignat*}{2} A_n &= \dfrac{1}{n}\Biggl[\Bigl(\dfrac{1}{n}\Bigr)^2 + \Bigl(\dfrac{2}{n}\Bigr)^2 + \dots + \Bigl(\dfrac{n}{n}\Bigr)^2\Biggr] \\ &= \dfrac{1}{n^3}\bigl(1^2 + 2^2 + \dots + n^2\bigr) \\ &= \dfrac{1}{n^3} \times \dfrac{1}{6}n(n+1)(2n+1) &\qquad&\text{(sum of the first \(n\) squares)} \\ &= \dfrac{1}{3} + \dfrac{1}{2n} + \dfrac{1}{6n^2}. \end{alignat*}

This is an upper Riemann sum for \(f\) on \([0,1]\).

Similarly, we can obtain a lower bound for the area of \(R\) by finding the total area \(B_n\) of the \(n\) rectangles \(L_1,L_2,\dots,L_n\):

\begin{alignat*}{2} B_n &= \dfrac{1}{n}\Biggl[\Bigl(\dfrac{0}{n}\Bigr)^2 + \Bigl(\dfrac{1}{n}\Bigr)^2 + \dots + \Bigl(\dfrac{n-1}{n}\Bigr)^2\Biggr] \\ &= \dfrac{1}{n^3}\bigl(0^2 + 1^2 + \dots + (n-1)^2\bigr) \\ &= \dfrac{1}{n^3} \times \dfrac{1}{6}(n-1)n(2n-1) &\qquad&\text{(sum of the first \(n-1\) squares)} \\ &= \dfrac{1}{3} - \dfrac{1}{2n} + \dfrac{1}{6n^2}. \end{alignat*}

This is a lower Riemann sum for \(f\) on \([0,1]\).

Since \(B_n \leq \,\text{Area }R\, \leq A_n\), we now have

\[ \dfrac{1}{3} - \dfrac{1}{2n} + \dfrac{1}{6n^2} \leq \,\text{Area }R\, \leq \dfrac{1}{3} + \dfrac{1}{2n} + \dfrac{1}{6n^2}. \]

By taking the limit as \(n\to \infty\), we see that the area of \(R\) is \(\dfrac{1}{3}\). We can take this as the definition of the area of \(R\).

Next page - Links forward - More on means