Answers to exercises

Exercise 1

1. There are \(3 \times 2 = 6\) terms in the expansion.
2. There are \(2^5 = 32\) terms in the expansion.

Exercise 2

\(c_2 =\dbinom{12}{2} = 66, \quad c_3 =\dbinom{12}{3} = 220, \quad c_5 =\dbinom{12}{5} = 792, \quad c_9 =\dbinom{12}{9} = 220\).

Exercise 3

The possible strings of \(R\)'s and \(U\)'s have length \(m+n\). If the grid has height \(m\) and width \(n\), then there must be \(m\) \(U\)'s and \(n\) \(R\)'s. So the number of ways of choosing the paths is \(\dbinom{m+n}{n} = \dbinom{m+n}{m}\).

Exercise 4

The binomial theorem gives

\[ (1+x)^n = \dbinom{n}{0}+ \dbinom{n}{1}x + \dbinom{n}{2}x^2+\dots+\dbinom{n}{r}x^r+\dots+ \dbinom{n}{n-1}x^{n-1} + \dbinom{n}{n}x^n. \]

1. When \(x=2\), we have
   \begin{align*} 3^n&=(1+2)^n \\ &= \dbinom{n}{0}+ \dbinom{n}{1}2 + \dbinom{n}{2}2^2+\dots+\dbinom{n}{r}2^r+\dots+ \dbinom{n}{n-1}2^{n-1} + \dbinom{n}{n}2^n\\ &=1+ 2\dbinom{n}{1}+ 4\dbinom{n}{2}+\dots+2^r\dbinom{n}{r}+\dots+ 2^{n-1}\dbinom{n}{n-1} + 2^n. \end{align*}
2. When \(x=-2\), we have
   \begin{align*} &(-1)^n =(1-2)^n \\ &= \dbinom{n}{0}+ \dbinom{n}{1}(-2) + \dbinom{n}{2}(-2)^2+\dots+\dbinom{n}{r}(-2)^r+\dots+ \dbinom{n}{n-1}(-2)^{n-1} + \dbinom{n}{n}(-2)^n\\ &=1 - 2\dbinom{n}{1}+ 4\dbinom{n}{2}+\dots+(-2)^r\dbinom{n}{r}+\dots+ (-2)^{n-1}\dbinom{n}{n-1} + (-2)^n. \end{align*}

Exercise 5

1. \((2x-3y)^4 = 16x^4 - 96x^3y + 216x^2y^2 - 216xy^3 + 81y^4\)
2. \(\Big(x-\dfrac{2}{x}\Big)^4 =24 + \dfrac{16}{x^4} - \dfrac{32}{x^2} - 8 x^2 +x^4\)

Exercise 6

There are eight terms in the expansion.

The general term is \((-2)^r\dbinom{7}{r}a^{7-r}b^{3r}\), for \(0\leq r\leq 7\).

Exercise 7

The constant term is 15.

Exercise 8

The middle term is \(-4320 x^3 y^3\).

Exercise 9

\(c_9=2^6\times3^9\dbinom{15}{9}=6\ 304\ 858\ 560\)

Exercise 10

In the following diagram, there are \(\tbinom{3+2}{3}\) paths from \(Y\) to \(X\), and \(\tbinom{3+2}{2}\) paths from \(X\) to \(W\). So the number of paths from \(Y\) to \(W\) that pass through \(X\) is

\[ \dbinom{3+2}{3} \dbinom{3+2}{2} =\dbinom{5}{3} \dbinom{5}{2} = \dbinom{5}{2}^2. \]

Every path from \(Y\) to \(W\) meets the diagonal, and so the total number of paths from \(Y\) to \(W\) can be found by summing the number of such paths through each point on the diagonal. The general result follows from the same argument.

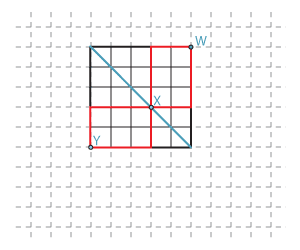
Detailed description of diagram

Exercise 11

Assume that the coefficients of three consecutive powers of \((1+x)^n\) are in arithmetic progression. Let the three coefficients be

\[ \dbinom{n}{r-1}, \qquad \dbinom{n}{r}, \qquad \dbinom{n}{r+1}. \]

Then

\begin{align*} \dbinom{n}{r} -\dbinom{n}{r-1} &= \dbinom{n}{r+1} -\dbinom{n}{r}\\ \dfrac{n!}{(n-r)!r!} - \dfrac{n!}{(n-r+1)!(r- 1)!} &= \dfrac{n!}{(n-r -1)!(r+1)!} - \dfrac{n!}{(n-r)!r!}\\ \dfrac{n!}{(n-r)!(r-1)!}\Bigg(\dfrac{1}{r}-\dfrac{1}{n-r+1}\Bigg) &= \dfrac{n!}{(n-r-1)!r!}\Bigg(\dfrac{1}{r+1}-\dfrac{1}{n-r}\Bigg)\\ \dfrac{n-2r+1}{n-r+1}&=\dfrac{n-2r-1}{r+1}\\ (n-2r)^2&=n+2. \end{align*}

For this to be possible, \(n+2\) is a perfect square.