Content
Further identities and results
Sum of the squares of the binomial coefficients
In the following diagram of Pascal's triangle, we see that by summing the squares of the
numbers in the fourth row,
\[ 1^2+ 4^2+6^2+4^2+1^2=70, \]we get the middle number of the eighth row.
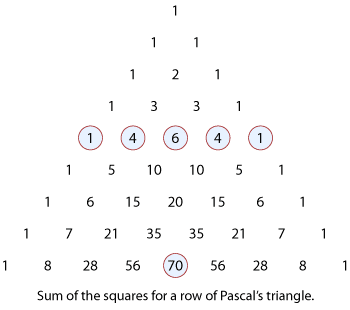
Detailed description of diagram
We now explain the general pattern.
Using the fact that
\[ \dbinom{n}{r} = \dbinom{n}{n-r}, \]we can write the binomial expansion in two different ways:
\begin{align*} (1+x)^n &= \dbinom{n}{0}+ \dbinom{n}{1}x + \dbinom{n}{2}x^2+\dots+\dbinom{n}{r}x^r+\dots+ \dbinom{n}{n-1}x^{n-1} + \dbinom{n}{n}x^n,\\ (1+x)^n &= \dbinom{n}{n}+ \dbinom{n}{n-1}x + \dbinom{n}{n-2}x^2+\dots+\dbinom{n}{r}x^{n-r}+\dots+ \dbinom{n}{1}x^{n-1} + \dbinom{n}{0}x^n. \end{align*}Multiplying these two expansions together, we see that in \((1+x)^n(1+x)^n\) the
coefficient of \(x^n\) is
\[ \dbinom{n}{0}^2 + \dbinom{n}{1}^2+\dots+\dbinom{n}{r}^2+\dots+\dbinom{n}{n}^2. \]Also, since
\[ (1+x)^n (1+x)^n = (1+x)^{2n}, \]the coefficient of \(x^n\) in this expansion is \(\dbinom{2n}{n}\). Equating the two expressions
for the coefficient of \(x^n\) we have
\[ \dbinom{2n}{n}= \dbinom{n}{0}^2 + \dbinom{n}{1}^2+\dots+ \dbinom{n}{r}^2+\dots+\dbinom{n}{n}^2. \]Using summation notation, this identity is
\[ \dbinom{2n}{n}=\sum_{r=0}^{n}\dbinom{n}{r}^2. \]The case for \(n = 4\) was given at the start of this section:
\[ \dbinom{8}{4} = \dbinom{4}{0}^2 + \dbinom{4}{1}^2+ \dbinom{4}{2}^2 + \dbinom{4}{3}^2+ \dbinom{4}{4}^2. \]Exercise 10
The number of forward paths from the bottom left to the top right of an \(n\times n\) grid
is \(\dbinom{2n}{n}\). Use an argument involving paths in the grid to prove
\[ \dbinom{2n}{n}= \dbinom{n}{0}^2 + \dbinom{n}{1}^2+\dots+ \dbinom{n}{r}^2+\dots+\dbinom{n}{n}^2. \](Hint. Draw a diagonal line across the grid from the top-left corner to the bottom-right corner. Choose a point of the grid on the diagonal line. Consider the number of forward paths from the bottom-left corner to the point and then the number of paths from the point to the top-right corner. Repeat for each point on the diagonal line.)
Yet more results and identities
We give some further results that come from applying the binomial theorem to \((1 + x)^n\).
Exercise 11
Each of the following expansions has three coefficients in arithmetic progression:
\begin{align*} (1+x)^7 &= 1+7x+21x^2+35x^3+35x^4+21x^5+7x^6+x^7,\\ (1+x)^{14} &= 1+14x+91x^2+364x^3+1001x^4+2002x^5+3003x^6+3432x^7+\dotsb,\\ (1+x)^{23} &= \dotsb + 490\,314 x^8 + 817\,190 x^9 + 1\,144\,066 x^{10} + \dotsb. \end{align*}In the first expansion, where \(n=7\), the arithmetic progression is 7, 21, 35.
In the second expansion, where \(n=14\), the progression is 1001, 2002, 3003.
For the expansion of \((1+x)^n\), where \(n>2\), prove that if the coefficients of three
consecutive powers are in arithmetic progression, then \(n+2\) is a perfect square.
(Hint. Consider three coefficients \(\dbinom{n}{r-1}\), \(\dbinom{n}{r}\), \(\dbinom{n}{r+1}\).)
Example
Prove the identity
\[ n\times2^{n-1}= \sum_{k=0}^{n}k\times\dbinom{n}{k} \]and check in the case when \(n=4\).
Solution
We begin with the expansion of \((1 + x)^n\) from the binomial theorem:
\[ (1+x)^n= \sum_{k=0}^{n}\dbinom{n}{k}x^k. \]Differentiating both sides of this identity with respect to \(x\) gives
\[ n(1+x)^{n-1}= \sum_{k=0}^{n}k\dbinom{n}{k}x^{k-1}. \]Now substitute \(x=1\) to obtain the result:
\[ n2^{n-1}= \sum_{k=0}^{n}k\dbinom{n}{k}. \]When \(n=4\), the left-hand side is \(4\times2^3 = 32\) and the right-hand side is
\begin{align*} 4+2\times\dbinom{4}{2} +3\times\dbinom{4}{3}+4 &=4+2\times6+3\times4+4\\ &=32. \end{align*}If we substitute \(x = -1\) into the identity from the previous example,
\[ n(1+x)^{n-1}= \sum_{k=0}^{n}k\dbinom{n}{k}x^{k-1}, \]then we obtain
\[ \sum_{k=0}^{n}k\dbinom{n}{k}(-1)^{k-1} = 0. \]For example, when \(n=6\) this gives
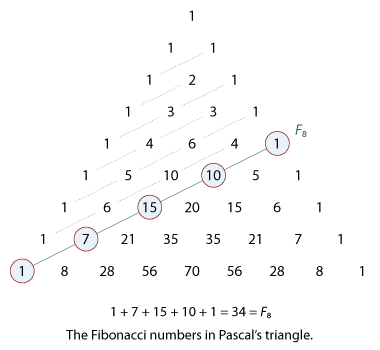
\[ \dbinom{6}{1} +3 \dbinom{6}{3} + 5\dbinom{6}{5} = 2\dbinom{6}{2} + 4\dbinom{6}{4}+ 6\dbinom{6}{6}. \]A link to the Fibonacci numbers
Let \(F(n)\) denote the sum
\[ F(n) = \dbinom{n}{0} + \dbinom{n-1}{1} + \dbinom{n-2}{2} + \dotsb \]where we keep summing until the lower number exceeds the top one. Then
\[ F(n+1) = \dbinom{n+1}{0} + \dbinom{n}{1} + \dbinom{n-1}{2} + \dotsb. \]Adding the first term in line 1 with the second in line 2 and so on, we get
\[ F(n+1) + F(n) = \dbinom{n+1}{0} + \Bigg[\dbinom{n}{0} + \dbinom{n}{1}\Bigg] + \Bigg[\dbinom{n-1}{1} + \dbinom{n-1}{2}\Bigg] + \dotsb. \]Using Pascal's identity, we obtain
\[ F(n+1)+F(n) = \dbinom{n+2}{0}+ \dbinom{n+1}{1}+ \dbinom{n}{2} +\cdots = F(n+2). \]Since \(F(0)=F(1)=1\), we have shown that \(F(0)\), \(F(1)\), \(F(2)\), \(F(3)\), \(\dots\) is the sequence of Fibonacci numbers.
This result can be demonstrated in terms of Pascal's triangle.