Assumed knowledge

• Basic skills for simplifying algebraic expressions.
• Expanding brackets.
• Factoring linear and quadratic expressions.
• Some experience in working with polynomials.

Motivation

I am the very model of a modern Major-General,
I've information vegetable, animal, and mineral,
I know the kings of England, and I quote the fights historical
From Marathon to Waterloo, in order categorical;
I'm very well acquainted, too, with matters mathematical,
I understand equations, both the simple and quadratical,
About binomial theorem I'm teeming with a lot o' news —
With many cheerful facts about the square of the hypotenuse.

— Gilbert and Sullivan, Pirates of Penzance.

When you look at the following expansions you can see the symmetry and the emerging patterns. The simple first case dates back to Euclid in the third century BCE.

\begin{align*} (a+b)^2 &= (a+b)(a+b)\\ &=a^2+2ab+b^2\\ \\ (a+b)^3 &= (a+b)^2(a+b)\\ &=(a^2+2ab+b^2)(a+b)\\ &=(a^3+2a^2b+ab^2) + (a^2b+2ab^2+b^3)\\ &=a^3+3a^2b+3ab^2+b^3\\ \\ (a+b)^4 &= (a+b)^3(a+b)\\ &=(a^3+3a^2b+3ab^2+b^3)(a+b)\\ &=(a^4+3a^3b+3a^2b^2+ab^3) + (a^3b+3a^2b^2+3ab^3+b^4)\\ &=a^4+4a^3b+6a^2b^2 +4ab^3+ b^4. \end{align*}

Notice that

• the expansion of \((a+b)^2\) has three terms and in each term the sum of the indices is 2
• the expansion of \((a+b)^3\) has four terms and in each term the sum of the indices is 3
• the expansion of \((a+b)^4\) has five terms and in each term the sum of the indices is 4.

We conjecture that the expansion of \((a+b)^n\) has \(n+1\) terms and in each term the sum of the indices is \(n\).

The coefficients of the terms follow an interesting pattern. How can we determine this pattern and how can we predict the coefficients of the expansion of \((a+b)^n\)? The binomial theorem gives us the general formula for the expansion of \((a+b)^n\) for any positive integer \(n\). It also enables us to determine the coefficient of any particular term of an expansion of \((a+b)^n\).

In this module, Pascal's triangle is centre stage. The coefficients of the expansion of \({(a+b)^n}\), for a particular positive integer \(n\), are contained in sequence in the \(n\)th row of this triangle of numbers. The triangular numbers, the square numbers and the numbers of the Fibonacci sequence can be found from the triangle, and many interesting identities can be established.

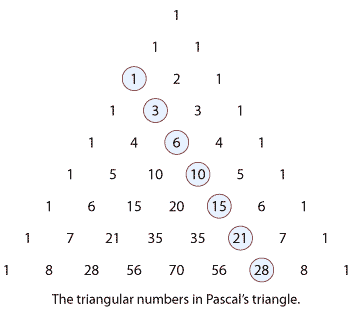
For example, the triangular numbers occur in Pascal's triangle along the diagonal shown in the following diagram. The square numbers can be found by adding pairs of adjacent numbers on this diagonal.

Detailed description of diagram

This topic combines combinatoric and algebraic results in a most productive manner.

The relationship between the expansion of \((a + b)^n\) and binomial probabilities is addressed in the module Binomial distribution .

Next page - Content - A look at Pascal's triangle