Answers to exercises

Exercise 1

Let \(A(x_1,y_1)\) and \(B(x_2,y_2)\) be two points. Assume that \(P(x,y)\) is on the interval \(AB\) with

\[ AP:PB = a:b = \tfrac{a}{b}:1. \]

So \(P\) divides \(AB\) in the ratio \(\dfrac{a}{b}:1\). Thus

\[ x = \dfrac{x_1+\dfrac{a}{b}x_2}{1+\dfrac{a}{b}} = \dfrac{bx_1+ax_2}{b+a} \]

and, similarly,

\[ y = \dfrac{by_1+ay_2}{b+a}. \]

Exercise 2

Without loss of generality, assume \(PB = 1\). Then

\begin{align*} AC &= AP\,\cos\theta\\ x-x_1 &= k\,\dfrac{x_2-x_1}{k+1}\\ (x-x_1)(k+1) &= kx_2-kx_1\\ x &= \dfrac{x_1+kx_2}{k+1}. \end{align*}

From the same diagram, we have \(CP = AP\,\sin\theta\). Proceed in a similar way to find \(y\).

Exercise 3

Detailed description

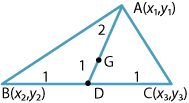
The midpoint \(D\) of \(BC\) is

\[ \Bigl(\dfrac{x_2+x_3}{2},\dfrac{y_2+y_3}{2}\Bigr). \]

The point \(G\) that divides the median \(AD\) in the ratio \(2:1\) is

\[ \Biggl(\dfrac{1}{3}\Bigl(x_1 + \dfrac{2(x_2+x_3)}{2}\Bigr), \dfrac{1}{3}\Bigl(y_1 + \dfrac{2(y_2+y_3)}{2}\Bigr)\Biggr) = \Biggl(\dfrac{x_1+x_2+x_3}{3}, \dfrac{y_1+y_2+y_3}{3}\Biggr). \]

This is symmetric in \(x_1,x_2,x_3\) and in \(y_1,y_2,y_3\). So \(G\) lies on the other medians \(BE\) and \(CF\), and the medians are concurrent.

Exercise 4

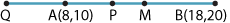
\(M\) is \((13,15)\).

\(P\) is \(\Bigl(\dfrac{3\times 8+2\times 18}{3+2}, \dfrac{3\times 10+2\times 20}{3+2}\Bigr) = (12,14)\).

\(Q\) is \(\Bigl(\dfrac{3\times 8-2\times 18}{3-2}, \dfrac{3\times 10-2\times 20}{3-2}\Bigr) = (-12,-10)\).

Thus

\begin{align*} MB^2 &= 5^2+5^2=50,\\ MP^2 &= 1^2+1^2=2,\\ MQ^2 &= 25^2+25^2=2\times 25^2. \end{align*}

Hence

\[ MP \cdot MQ = \bigl(2\times 2\times 25^2\bigr)^{\frac{1}{2}} = 50 = MB^2. \]

Exercise 5

1. \(\text{Gradient} = \dfrac{\dfrac{c}{q}-\dfrac{c}{p}}{cq-cp} = \dfrac{p-q}{pq(q-p)} = -\dfrac{1}{pq}\)
2. \(\text{Gradient} = \dfrac{2aq-2ap}{aq^2-ap^2} = \dfrac{2(q-p)}{(q-p)(q+p)} = \dfrac{2}{p+q}\)
3. \(\text{Gradient} = \dfrac{b\sin\phi-b\sin\theta}{a\cos\phi-a\cos\theta} = \dfrac{2b\,\cos\bigl(\dfrac{\phi+\theta}{2}\bigr)\,\sin\bigl(\dfrac{\phi-\theta}{2}\bigr)} {2a\,\sin\bigl(\dfrac{\phi+\theta}{2}\bigr)\,\sin\bigl(\dfrac{\theta-\phi}{2}\bigr)} = -\dfrac{b}{a}\cot\Bigl(\dfrac{\phi+\theta}{2}\Bigr)\)

Exercise 6

1. The lines \(4x+3y-6=0\) and \(x-2y-7=0\) meet where \(11y+22=0\), so \(y=-2\) and \(x=3\). The line through \((3,-2)\) parallel to the \(x\)-axis is \(y=-2\).
2. The lines \(3x+2y=2\) and \(4x+3y=7\) meet where \(y=13\) and \(x=-8\). So the gradient is \(\dfrac{13-3}{-8-2}=-1\).

Exercise 7

The angle sum formulas give

\begin{align*} \sin(\theta+90^\circ) &= \sin\theta\,\cos 90^\circ + \cos\theta\,\sin 90^\circ = \cos\theta\\ \cos(\theta+90^\circ) &= \cos\theta\,\cos 90^\circ - \sin\theta\,\sin 90^\circ = -\sin\theta. \end{align*}

Thus

\[ \tan(90^\circ+\theta) = \dfrac{\cos\theta}{-\sin\theta} = -\dfrac{1}{\tan\theta}. \]

Suppose \(y=mx\) is perpendicular to \(y=m_1x\). Then \(m=\tan\theta\) and \(m_1=\tan(90^\circ +\theta)\). So

\[ m_1=-\dfrac{1}{m} \]

and therefore \(mm_1=-1\).

Conversely, suppose \(mm_1=-1\), where \(m =\tan\theta\). Then

\[ m_1 = -\dfrac{1}{\tan\theta} = \tan(90^\circ + \theta). \]

So \(y=mx\) is perpendicular to \(y=m_1x\).

Exercise 8

1. All lines parallel to \(ax+by+c = 0\) have equation \(ax+by+d = 0\), for some \(d\). If \(P(x_1,y_1)\) lies on the line, then \(ax_1+by_1+d = 0\). So the equation is \(ax+by = ax_1+by_1\).
2. All lines perpendicular to \(l\) have equation \(bx-ay+d = 0\), for some \(d\). If \(P(x_1,y_1)\) lies on the line, then \(bx_1-ay_1+d = 0\). So the equation is \(bx-ay = bx_1-ay_1\).

Exercise 9

1. The perpendicular distance of \((1,2)\) from the line \(x+2y-10=0\) is
   \[ \dfrac{|1+4-10|}{\sqrt{1^2+2^2}} = \sqrt{5}, \] which equals the radius. Therefore the line is tangent to the circle.
2. The perpendicular distance of \((1,2)\) from the line \(x+2y-12=0\) is
   \[ \dfrac{|1+4-12|}{\sqrt{1^2+2^2}} = \dfrac{7}{\sqrt{5}} = \dfrac{7\sqrt{5}}{5}, \] which is greater than the radius \(\sqrt{5}\). Hence the line does not touch the circle.

Exercise 10

Detailed description

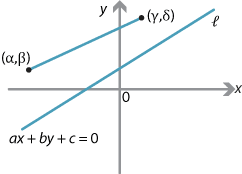
Note that a point \((x_1,y_1)\) lies on the line \(l\) if and only if \(ax_1+by_1+c = 0\).

Suppose that points \((\alpha,\beta)\) and \((\gamma,\delta)\) are on the same side of \(l\). Then the line segment from \((\alpha,\beta)\) and \((\gamma,\delta)\) does not cross \(l\). So \(ax_1+by_1+c \ne 0\) for each point \((x_1,y_1)\) on the line segment. Thus the expression \(ax_1+by_1+c\) cannot change sign as the point \((x_1,y_1)\) moves along the line segment from \((\alpha,\beta)\) to \((\gamma,\delta)\). Hence the signs of \(a\alpha+b\beta+c\) and \(a\gamma+b\delta+c\) are the same.

Points on different sides of \(l\) must have different signs, as it is possible to choose \((x_1,y_1)\) so that \(ax_1+by_1+c > 0\), and choose \((x_2,y_2)\) so that \(ax_2+by_2+c < 0\).

Exercise 11

\begin{align*} (x+1)^2+(y-6)^2 &= (x-3)^2+(y-4)^2\\ x^2+2x+1+y^2-12y+36 &= x^2-6x+9+y^2-8y+16\\ 2x-12y+37 &= -6x-8y+25\\ 8x-4y+12 &=0\\ 2x-y+3 &= 0 \end{align*}

Exercise 12

The area of the triangle is

\[ \Bigl|\dfrac{1}{2}\bigl(6(5-7)+8(3-5)+2(7-3)\bigr)\Bigr| = \Bigl|\dfrac{-12-16+8}{2}\Bigr| = 10. \]

Exercise 13

Detailed description

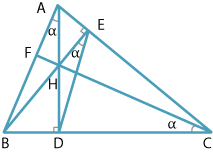
Let \(AD\) be the altitude perpendicular to \(BC\), let \(BE\) be the altitude perpendicular to \(AC\) and let \(AD\) meet \(BE\) at \(H\). Finally let \(CH\) meet \(AB\) at \(F\). We must prove \(FC\) is perpendicular to \(AB\).

Join \(DE\). Let \(\alpha = \angle BCF\). Then \(ECDH\) is a cyclic quadrilateral (supplementary opposite angles), so \(\angle DEH=\alpha\) (angles in the same segment).

Similarly, \(AEBD\) is a cyclic quadrilateral and \(\angle DAB=\alpha\).

From \(\triangle ABD\), \(\angle ABD=180^{\circ} -90^{\circ} -\alpha=90^{\circ} -\alpha\). Finally, in \(\triangle CBF\), \(\angle BFC+\alpha+90^{\circ} -\alpha=180^{\circ}\), so \(\angle BFC=90^{\circ}\), as required.

Exercise 14

Let \(A = (a,b)\) and \(B = (c,d)\). The midpoint \(M\) of \(AB\) is \((2,3)= \Bigl(\dfrac{a + c}{2}, \dfrac{b + d}{2}\Bigr)\), so

\begin{alignat*}{2} a + c &= 4 &\qquad&(1)\\ b + d &= 6. &&(2) \end{alignat*}

Since the point \(A(a,b)\) lies on the line \(2x + y - 3 = 0\) and the point \(B(c,d)\) lies on the line \(3x - 2y + 1 = 0\), we also have

\begin{alignat*}{2} 2a + b &= 3 &\qquad&(3)\\ 3c - 2d &= -1. &&(4) \end{alignat*}

From (1) and (2), we have \(c = 4 - a\) and \(d = 6 - b\). Substituting these into (4) gives

\[ 3a -2b = 1.\qquad (5) \]

We can now solve (3) and (5) to obtain \(a = 1\) and \(b = 1\).

We have found that \(A\) is \((a,b) = (1,1)\). So the gradient of the line \(l\) is \(m = \dfrac{1-3}{1-2} = 2\). Thus \(l\) has equation \(y - 1 = 2(x - 1)\) or, equivalently, \(y = 2x - 1\).