Links forward
Quadratic equations and the conics
The general linear equation
\[ ax+by+c=0, \]where \(a\) or \(b\) is non-zero, is the equation of a line in \(\mathbb{R}^2\). So it is natural to ask the question:
What curves in \(\mathbb{R}^2\) occur as the graph of the general quadratic equation in two variables?
Consider the set
\[ S = \bigl\{\, (x,y)\in \mathbb{R}^2 \bigm| ax^2+2hxy+by^2+2gx+2fy+c=0 \,\bigr\}, \] where \(a,b,c,f,g,h\) are constants and at least one of \(a\), \(h\) and \(b\) is non-zero. The 2's in the equation are somewhat mysterious, but are related to completing the square.There are several approaches to studying such sets \(S\), including conic sections and the focus–directrix definition, but we will leave them to the module Quadratics. In this section, we will simply give a picture gallery of typical examples.
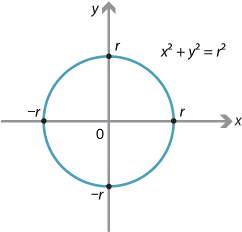
Example 1 (Circle)
The graph of \(x^2+y^2 = r^2\) is the circle with centre the origin and radius \(r\).
Example 2 (Empty set)
The graph of \(x^2+y^2 = -1\) is the empty set.
Example 3 (Two lines)
The equation \(x^2-y^2 = 0\) factorises as \((x+y)(x-y) = 0\), so \(y = -x\) or \(y = x\). So this example is the union of two lines.
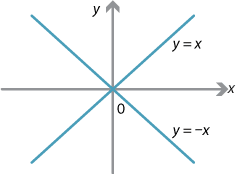
Example 4 (One line)
The equation \(x^2-2xy+y^2 = 0\) factorises as \((y-x)^2 = 0\), which is just one line!
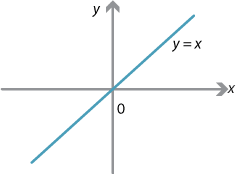
Example 5 (One point)
The graph of \((x-f)^2+(y-g)^2 = 0\) is just the single point \((f,g)\).
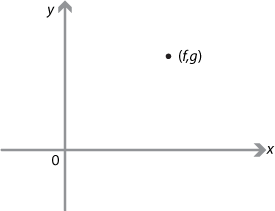
Example 6 (Rectangular hyperbola)
The graph of \(xy = 1\) is called a rectangular hyperbola.
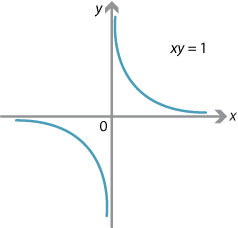
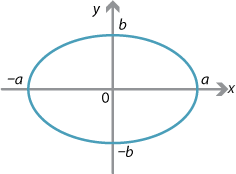
Example 7 (Ellipse)
The graph of
\[ \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2} = 1, \qquad \text{for \(a>0\), \(b>0\),} \] is an ellipse. It is a circle if \(a=b\).
Example 8 (Hyperbola)
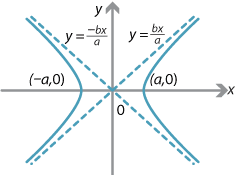
Consider the quadratic equation
\[ \dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1, \qquad \text{for \(a>0\), \(b>0\).} \]By setting \(x=0\), we see there are no \(y\)-intercepts. If \(y=0\), then \(x=\pm a\).
As \(x\to\infty\), \(y\to\pm\infty\) and the curve approaches the lines \(y = \dfrac{bx}{a}\) or \(y = -\dfrac{bx}{a}\), which are called the asymptotes of the curve.
This is a (general) hyperbola. It is a rectangular hyperbola if \(a=b\).
If the rectangular hyperbola \(xy=1\) from Example 6 is rotated through \(45^\circ\), it becomes \(\dfrac{x^2}{2}-\dfrac{y^2}{2}=1\), which is recognisable as a hyperbola.
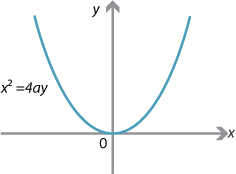
Example 9 (Parabola)
The graph of \(x^2=4ay\), for \(a>0\), is a parabola. It has no asymptotes.
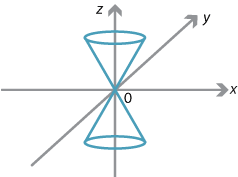
The set of points in \(\mathbb{R}^3\) satisfying \(x^2+y^2=z^2\) forms a cone (perhaps better described as a double cone), as shown in the following diagram.
A horizontal plane meets the cone in either one point or a circle. All the other examples in our picture gallery (except the empty set) occur when different planes intersect the cone! It is educative to try and visualise them all. For this reason the ellipse, the parabola, the hyperbola and the circle are often called the conic sections. Several of the Greek mathematicians followed this approach to the conics.
The general quadratic in two variables \(x\) and \(y\) is
\[ S = \bigl\{\, (x,y)\in \mathbb{R}^2 \bigm| ax^2+2hxy+by^2+2gx+2fy+c=0 \,\bigr\}. \]If we apply a translation, a rotation or a reflection to \(S\), then we do not change the intrinsic geometrical nature of \(S\). Unless \(a = b = 0\) (in which case \(S\) is a rectangular hyperbola), a rotation can be found which reduces \(S\) to either
\[ a_1x^2+b_1y^2+2g_1x+2f_1y+c_1 = 0 \qquad \text{or} \qquad a_1x^2+2g_1x+2f_1y+c_1 = 0. \]In the second case, completing the square in \(x\) leads to
\[ a_2x^2+2f_2y+c_2 = 0, \]which is a parabola. In the first case, completing the square in both \(x\) and \(y\) leads to
\[ a_2x^2+b_2y^2 = c_2, \]which is either a hyperbola, an ellipse, a circle, two lines, one line, one point or the empty set, depending on the values of \(a_2\), \(b_2\) and \(c_2\).
Next page - History and applications
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |