Links forward

Three-dimensional coordinate geometry

The principal elements in solid geometry (3-dimensional geometry) are points, lines and planes. In the plane (2-dimensional geometry), the `incidence' properties are very straightforward:

two points determine a line
two lines are parallel or meet at a unique point.

In 3-dimensional space, things are more complicated:

two points still determine a line
two lines meet or are parallel or are skew.

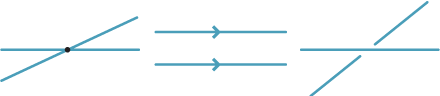
A pair of crossing lines, one pair of parallel lines, one pair of skew lines.

To visualise a pair of skew lines, think of one as being `behind' the other.

Three points which are not collinear determine a unique plane. But there are an infinite number of planes through a fixed line or three collinear points.

Two planes are parallel or meet in a line. Indeed, if two planes have a point in common, they must have a whole line of points in common (this is not obvious).

To set up a coordinate system for solid geometry, choose a plane \(0xy\) and then fix axes \(0x\) and \(0y\) as in plane geometry.

Three dimensional axes, x y and z.

The axis \(0z\) is the normal to the plane \(0xy\) through the origin. Usually we choose \(0z\) to come out of the standard \(x\)–\(y\) plane. (This is called a right-handed coordinate system and is very important when vectors are used — especially in applications in physics.)

Thus \(0x\perp 0y\), \(0x\perp 0z\) and \(0y\perp 0z\).

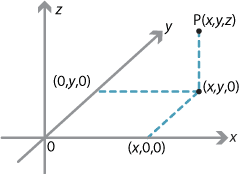
Three dimensional axes, x y and z. Points (x, 0, 0), (0, y, 0), (x, y, 0), P(x, y, z) marked.
Detailed description

Every point in 3-space is a certain distance \(z\) above the \(x\)–\(y\) plane (if \(z<0\), the point is below). The points in the \(0xy\) plane are given the coordinates \((x,y,0)\) and, in general, \(P\) is \((x,y,z)\).

Midpoints and distance

Let \(P(x_1, y_1, z_1)\) and \(Q(x_2, y_2, z_2)\) be points in \(\mathbb {R}^3\). Then:

The midpoint of the line segment \(PQ\) is \(M\Bigl(\dfrac{x_1+x_2}{2}, \dfrac{y_1 + y_2}{2}, \dfrac{z_1 + z_2}{2}\Bigr)\).
The distance between \(P\) and \(Q\) is \(\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\).

So, for example, in the above diagram \(OP^2=x^2+y^2+z^2\).

Lines in \(\mathbb{R}^3\)

To describe the points on a line, it is easiest to use a parameter which varies as a point moves along the line.

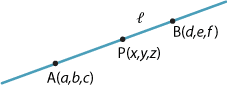
Line l with points A(a, b, c), P(x, y, z) and B(d, e, f)

Consider the line \(l\) through the fixed points \(A(a,b,c)\) and \(B(d,e,f)\). Let \(P(x,y,z)\) be any point on \(l\). Then the vector \((x-a,y-b,z-c)\) is a scalar multiple \(t\) of the vector \({(d-a,e-b,f-c)}\). So

\begin{align*} x-a &= t(d-a)\\ y-b &= t(e-b)\\ z-c &= t(f-c) \end{align*} and thus \begin{align*} x &= td+(1-t)a\\ y &= te+(1-t)b\\ z &= tf+(1-t)c, \end{align*} for \(t\in \mathbb{R}\). This is the parametric form for a line in \(\mathbb{R}^3\). If \(t=0\), then \(P=A\) and, if \(t=1\), then \(P=B\).

We can obtain the Cartesian form for the line by eliminating \(t\). It is

\[ \dfrac{x-a}{d-a} = \dfrac{y-b}{e-b} = \dfrac{z-c}{f-c}. \]

Parametric forms for curves in \(\mathbb{R}^2\) are discussed in the module Quadratics.

Planes in \(\mathbb{R}^3\)

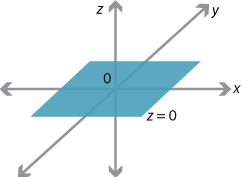
There are three principal planes in \(\mathbb{R}^3\). The \(x\)–\(y\) plane, which contains the axes \(0x\) and \(0y\), is given by

\[ \Pi_z = \bigl\{\, (x,y,z)\in \mathbb{R}^3 \bigm| z=0 \,\bigr\}. \]

The other two principal planes are \(x=0\) and \(y=0\).

Three dimensional axes, x y and z. Plane z = 0 shown.

Consider the set

\[ \Pi = \bigl\{\, (x,y,z)\in \mathbb{R}^3 \bigm| 3x+2y=6 \,\bigr\}. \]

If \(z=0\), then this restricts to a line in the \(x\)–\(y\) plane.

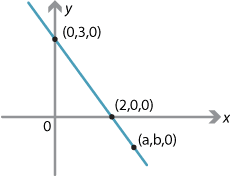
Line with points (0, 3, 0), (2, 0, 0) and (a, b, 0) shown.

However, if \((a,b,0)\) is any point on this line, then \((a,b,z)\in\Pi\) for any value of \(z\). Thus \(\Pi\) is a plane in \(\mathbb{R}^3\). Indeed \(\Pi\) is a plane parallel to the \(z\)-axis. In a similar way, \(3y+2z=6\) is a plane parallel to the \(x\)-axis, and \(3x+2z=6\) is a plane parallel to the \(y\)-axis.

Now consider the set

\[ \Pi = \bigl\{\, (x,y,z)\in \mathbb{R}^3 \bigm| 3x+2y+4z=12 \,\bigr\}. \]

Given the previous examples, it should be no surprise that this is a plane. Clearly it passes through the points \((4,0,0)\), \((0,6,0)\) and \((0,0,3)\), so the plane has three intercepts!

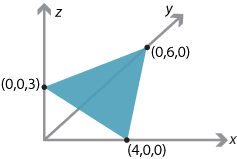
Three axes x, y and z are drawn and the points (0, 0, 3), (4, 0, 0) and (0, 6, 0) marked. Plane through these points is shaded.

The general equation for a plane is

\[ \Pi = \bigl\{\, (x,y,z)\in \mathbb{R}^3 \bigm| ax+by+cz=d \,\bigr\}, \] where at least one of \(a,b,c\) is non-zero.

So, in some ways, the general plane in \(\mathbb{R}^3\) is analogous to the line in \(\mathbb{R}^2\). To prove the above facts about planes, it is best to use vectors to represent the points in the plane.

Next page - Links forward - Quadratic equations and the conics