Content
Geometrical proofs using coordinate methods
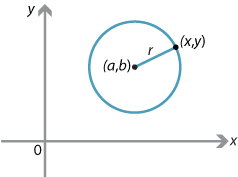
If a point \(P(x,y)\) lies on the circle with centre \((a,b)\) and radius \(r\), then Pythagoras' theorem gives
\[ (x-a)^2+(y-b)^2 = r^2. \]Conversely, if \(P(x,y)\) satisfies the equation above, then \(P\) lies on the circle with centre \((a,b)\) and radius \(r\).
This is an example of a locus problem.
A locus is the set of all points satisfying a geometrical condition. For example, a circle is the locus of all points a fixed distance \(r\) from a fixed point \((a,b)\).
Example
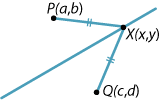
Let \(P(a,b)\) and \(Q(c,d)\) be two points in the plane. Find the equation of the line \(l\) that is the perpendicular bisector of the line segment \(PQ\).
Solution
First assume that \(a \ne c\) and \(b \ne d\). The gradient of \(PQ\) is \(\dfrac{b-d}{a-c}\), and so the gradient of the perpendicular line \(l\) is
\[ m = \dfrac{c-a}{b-d}. \]The line \(l\) goes through the midpoint \(\Bigl(\dfrac{a+c}{2},\dfrac{b+d}{2}\Bigr)\) of \(PQ\). Thus the equation of \(l\) is
\begin{align*} y-\dfrac{b+d}{2} &= m\Bigl(x-\dfrac{a+c}{2}\Bigr)\\ (b-d)(2y-b-d) &= (c-a)(2x-a-c)\\ 2(b-d)y+(d^2-b^2) &= 2(c-a)x+(a^2-c^2)\\ 2(b-d)y+2(a-c)x &= a^2+b^2-c^2-d^2. \end{align*}The final equation above is a sensible symmetric form for the equation of the perpendicular bisector of \(PQ\). This equation is also correct in the case that \(a = c\) or \(b = d\).
Alternatively, the question can be answered by finding the locus of all points \(X(x,y)\) equidistant from \(P(a,b)\) and \(Q(c,d)\).
\begin{align*} & PX = QX\\ \iff \ {}& PX^2 = QX^2\\ \iff \ {}& (x-a)^2+(y-b)^2 = (x-c)^2+(y-d)^2\\ \iff \ {}& -2ax-2by+a^2+b^2 = -2cx-2dy+c^2+d^2\\ \iff \ {}& 2(b-d)y+2(a-c)x = a^2+b^2-c^2-d^2. \end{align*}Note that the locus method involves less algebra.
Exercise 11
Use the locus method illustrated in the previous example to find the equation of the perpendicular bisector of the line segment \(PQ\), where the coordinates of \(P\) and \(Q\) are \((-1, 6)\) and \((3,4)\).
Example
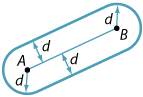
What is the locus of all points distance \(d\) from the fixed interval \(AB\)?
Solution
This is not meant to be a problem in coordinate geometry!
The locus is two intervals parallel to \(AB\) together with two semicircles of radius \(d\) with centres \(A\) and \(B\).
Example
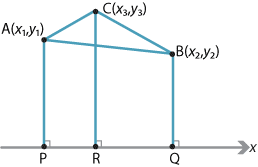
What is the area of the triangle with vertices \(A(x_1,y_1)\), \(B(x_2,y_2)\) and \(C(x_3,y_3)\)? Assume that \(C\) is above the interval \(AB\) as shown.
Solution
Let \(P(x_1,0)\), \(Q(x_2,0)\) and \(R(x_3,0)\) be the projections of \(A\), \(B\) and \(C\) onto the \(x\)-axis. We express the area of the triangle \(ABC\) in terms of three trapezia:
\begin{align*} \text{Area } \triangle ABC &= \text{Area } APRC + \text{Area } CRQB - \text{Area } APQB\\ &=\dfrac{1}{2}\bigl((y_1+y_3)(x_3-x_1)+(y_3+y_2)(x_2-x_3)-(y_1+y_2)(x_2-x_1)\bigr)\\ &=\dfrac{1}{2}\bigl(y_1(x_3-x_1-x_2+x_1)+y_2(x_2-x_3-x_2+x_1)+y_3(x_3-x_1+x_2-x_3)\bigr)\\ &=\dfrac{1}{2}\bigl(y_1(x_3-x_2)+y_2(x_1-x_3)+y_3(x_2-x_1)\bigr). \end{align*}The formula found in the previous example gives a negative value if \(C\) is below \(AB\). In general, the area of the triangle with vertices \(A(x_1,y_1)\), \(B(x_2,y_2)\), \(C(x_3,y_3)\) is
\[ \text{Area } \triangle ABC = \Bigl| \dfrac{1}{2} \bigl(y_1(x_3-x_2)+y_2(x_1-x_3)+y_3(x_2-x_1)\bigr)\Bigr|. \] Note. For readers familiar with determinants, the area of the triangle is \(\left|\dfrac{1}{2}\Delta\right|\), where \[ \Delta = \begin{vmatrix} 1&1&1\\ x_1&x_2&x_3\\ y_1&y_2&y_3 \end{vmatrix}. \]Exercise 12
Three points \(A(3,6)\), \(B(7,8)\) and \(C(5,2)\) are the vertices of \(\triangle ABC\). Find the area of this triangle using the formula given above.
Example
Use coordinate geometry to show that the altitudes of a triangle \(ABC\) are concurrent (at the orthocentre of the triangle).
Solution
By choosing the \(x\)-axis to be the line \(AB\) and the \(y\)-axis to be the line \(OC\), we can assume \(A(a,0)\), \(B(b,0)\) and \(C(0,c)\) are the vertices of the triangle \(ABC\), as shown in the following diagram.
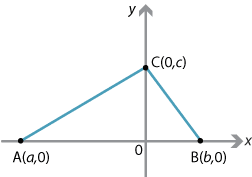
The gradient of \(BC\) is \(-\dfrac{c}{b}\), so the gradient of the altitude through \(A\) is \(\dfrac{b}{c}\). Thus the equation of the altitude through \(A\) is
\[ y = \dfrac{b}{c}(x-a). \]To find the \(y\)-intercept of the altitude, take \(x=0\), which implies \(y=-\dfrac{ba}{c}\). By swapping \(a\) and \(b\), we get \(-\dfrac {ab}{c}=-\dfrac{ba}{c}\). So the altitude through \(B\) has the same \(y\)-intercept. The altitude through \(C\) is the \(y\)-axis. Thus \(H=\Bigl(0,-\dfrac{ab}{c}\Bigr)\) lies on all three altitudes.
Exercise 13
Find a proof that the three altitudes of a triangle are concurrent using classical Euclidean geometry.
Exercise 14
Let \(M\) be the point \((2,3)\) and let \(l\) be a line through \(M\) which meets \(2x+y-3=0\) at \(A\) and meets \(3x-2y+1=0\) at \(B\). If \(M\) is the midpoint of \(AB\), find the equation of \(l\).
Next page - Links forward - Three-dimensional coordinate geometry