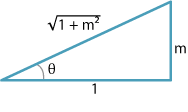Content
Perpendicular distances
Given a line \(l\) and a point \(P\) not on the line, it is natural to ask the question: What is the distance \(d\) of \(P\) from \(l\)?
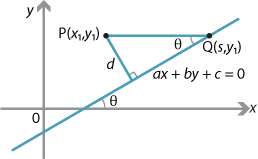
Assume that \(l\) has equation \(ax+by+c=0\), with \(a\ne0\) and \(b\ne 0\). We will also assume that the gradient \(m\) of \(l\) is positive. So the angle \(\theta\) between \(l\) and the positive \(x\)-axis is acute.
Let \(P(x_1,y_1)\) be any point, and let \(Q(s,y_1)\) be the point where the line \(l\) meets the line through \(P\) parallel to the \(x\)-axis. Since \(Q\) lies on the line \(l\), we have \(as+by_1+c=0\) and so
\[ s = \dfrac{-by_1-c}{a}. \]Thus
\[ PQ = |x_1-s| = \Bigl|\dfrac{ax_1+by_1+c}{a}\Bigr|. \]We can draw the following triangle, as \(m=\tan\theta\) with \(\theta\) acute.
From the triangle, we have
\[ \sin\theta = \dfrac{m}{\sqrt{1+m^2}}. \]Since \(m = -\dfrac{a}{b}\), this implies that
\[ \sin^2\theta = \dfrac{m^2}{1+m^2} = \dfrac{a^2}{a^2+b^2}. \]We are assuming that \(\theta\) is acute, so \(\sin \theta\) is positive and therefore
\[ \sin\theta = \dfrac{|a|}{\sqrt{a^2+b^2}}. \]From the first diagram, we now have
\[ d = PQ\,\sin\theta = \dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}. \]Theorem
Let \(P(x_1,y_1)\) be a point and let \(l\) be the line with equation \(ax+by+c=0\). Then the distance \(d\) from \(P\) to \(l\) is given by
\[ d = \dfrac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}. \]Proof
We have checked that the formula holds when \(a \ne 0\), \(b \ne 0\) and \(m > 0\). Check that the formula also holds when \(a=0\), when \(b=0\) and when \(m < 0\).
\(\Box\)
Example
What is the distance \(d\) of the point \(P(-6,-7)\) from the line \(l\) with equation \(3x+4y=11\)?
Solution
Here \(a=3\), \(b=4\), \(c=-11\), \(x_1=-6\) and \(y_1=-7\). So
\[ d = \dfrac{\bigl|-18-28-11\bigr|}{\sqrt{3^2+4^2}} = \dfrac{57}{5}. \]Exercise 9
A circle has centre \((1,2)\) and radius \(\sqrt{5}\).
- Find the perpendicular distance from the centre of the circle to the line with equation \(x+2y-10=0\) and hence show this line is a tangent to the circle.
- Find the perpendicular distance from the centre of the circle to the line with equation \(x+2y-12=0\) and hence show the line does not meet the circle.
Exercise 10
Consider a line \(l\) with equation \(ax+by+c=0\). Show that the expression \(ax_1+by_1+c\) is positive for \((x_1,y_1)\) on one side of the line \(l\) and negative for all points on the other side.
Next page - Content - Geometrical proofs using coordinate methods