Content

Parallel, intersecting and perpendicular lines

The axioms for Euclidean geometry include: Two lines meet at a point or are parallel.

Two lines n and l crossing and two lines l and n parallel.

Amongst those pairs of lines which meet, some are perpendicular.

Two lines l and n perpendicular.

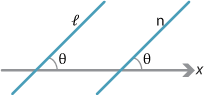
If lines \(l\) and \(n\) are not vertical, then they are parallel if and only if they have the same gradient \(m=\tan\theta\).

Two parallel lines with angle of inclination of theta to the horizontal.

Clearly, two horizontal lines are parallel. Also, any two vertical lines are parallel.

If lines \(l\) and \(n\) are not parallel, then their point of intersection can be found by solving the equations of the two lines simultaneously.

Example

Determine whether the following pairs of lines are parallel or identical and, if they are not, find the (unique) point of intersection:

  1. \(\begin{aligned}[t] y &= x+3\\ y &= x+6 \end{aligned}\)
  2. \(\begin{aligned}[t] y &= x+3\\ 3y &= 3x+7 \end{aligned}\)
  3. \(\begin{aligned}[t] y &= x+3\\ 5y &= 5x+15 \end{aligned}\)
  4. \(\begin{aligned}[t] y &= x+3\\ 2y &= x-2. \end{aligned}\)

Solution

  1. Both lines have gradient \(m=1\), but they have different \(y\)-intercepts. So the two lines are parallel.
  2. The lines \(y=x+3\) and \(y=x+\dfrac{7}{3}\) have the same gradient and are therefore parallel.
  3. The line \(5y=5x+15\) can also be written as \(y=x+3\). So the two lines are the same.
  4. Number the equations: \begin{alignat*}{2} y &= x+3 &\qquad&(1)\\ 2y &= x-2. &&(2) \end{alignat*} Substituting (1) into (2) gives \(2(x+3)=x-2\), so \(2x+6=x-2\). Therefore \(x=-8\) and \(y=-5\), and the point of intersection is \((-8,-5)\).

Exercise 6

  1. Find the equation of the line parallel to the \(x\)-axis which passes through the point where the lines \(4x+3y-6=0\) and \(x-2y-7=0\) meet.
  2. Find the gradient of the line which passes through the point \((2,3)\) and the point of intersection of the lines \(3x+2y=2\) and \(4x+3y=7\).

Screencast of exercise 6 mp4 of screencast of exercise 6

Perpendicular lines

All vertical lines \(x=a\) are perpendicular to all horizontal lines \(y=b\). So, in the following, we discuss lines with equations \(y=mx+b\), where \(m\ne0\).

Theorem

The lines \(y=mx+b\) and \(y=m_1x+c\) are perpendicular if and only if \(mm_1=-1\).

Proof

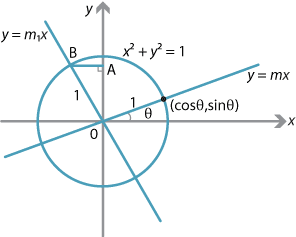
It is sufficient to prove that \(y=mx\) is perpendicular to \(y=m_1x\) if and only if \(mm_1=-1\).

Circle x squared plus y square = 1.
Detailed description

Suppose \(y=mx\) meets the \(x\)-axis at angle \(\theta\), that is, \(m=\tan\theta\). For convenience, assume that \(m>0\). Then \(y=mx\) meets the unit circle at \((\cos\theta,\sin\theta)\) in the first quadrant. If \(y=m_1x\) is perpendicular to \(y=mx\), then \(\angle AOB=\theta\), \(AB=\sin\theta\), \(OA=\cos\theta\) and \(B\) is \((-\sin\theta,\cos\theta)\). So

\[ m_1 = \dfrac{\cos\theta}{-\sin\theta} = -\dfrac{1}{\tan\theta} = -\dfrac{1}{m}, \]

as required.

Conversely, suppose \(mm_1=-1\) and \(m=\tan\theta\). Then

\[ m_1 = -\dfrac{1}{\tan\theta} = -\dfrac{\cos\theta}{\sin\theta} = \dfrac{\sin \bigl(\dfrac{\pi}{2}+ \theta\bigr)}{\cos\bigl(\dfrac{\pi}{2}+\theta \bigr)} = \tan\Bigl(\dfrac{\pi}{2}+\theta\Bigr). \]

Hence \(y=mx\) is perpendicular to \(y=m_1x\).

\(\Box\)

This result is often stated as:

The line \(y=m_1x+c_1\) is perpendicular to the line \(y=m_2x+c_2\) if and only if \(m_1m_2=-1\).

Exercise 7

Use the angle sum formulas

\begin{align*} \sin(A+B) &= \sin A\,\cos B+\cos A\,\sin B\\ \cos(A+B) &= \cos A\,\cos B-\sin A\,\sin B \end{align*} to show that \[ \tan(90^\circ+\theta) = -\dfrac{1}{\tan\theta}. \]

Then use this identity to give an alternative proof that lines \(y=mx\) and \(y=m_1x\) are perpendicular if and only if \(mm_1=-1\).

Example

Find the equation of the line \(l\) through \((1,3)\) perpendicular to the line \(2x+3y=12\). Find the equation of the line through \((4,5)\) parallel to \(l\).

Solution

The gradient of the line \(2x+3y=12\) is \(-\dfrac{2}{3}\), so \(l\) has gradient \(\dfrac{3}{2}\). The equation of \(l\) is

\begin{align*} y-3 &= \dfrac{3}{2}(x-1)\\ 2y-6 &= 3x-3\\ 3x-2y+3 &= 0. \end{align*}

The other line has equation \(y-5=\dfrac{3}{2}(x-4)\) or, equivalently, \(3x-2y-2=0\).

Example

For each pair of lines, determine whether they are parallel, identical or meet. If they meet, find the point of intersection and whether they are perpendicular.

  1. \(l:\ 3x=2y+5,\quad n:\ 2x+3y=7\)
  2. \(l:\ 6x=5y+7,\quad n:\ 12x=10y+13\)
  3. \(l:\ 3y=2x-1,\quad n:\ 4x=5y-7\)
  4. \(l:\ 5y=2x+2,\quad n:\ 15y-6x-6=0\)

Solution

  1. The gradient of \(l\) is \(\dfrac{3}{2}\) and the gradient of \(n\) is \(-\dfrac{2}{3}\). Since \[ \dfrac{3}{2}\times -\dfrac{2}{3} = -1, \] the lines are perpendicular.
    We have \begin{alignat*}{2} 6x &= 4y+10 &\qquad&\text{from \(l\),}\\ 6x+9y &= 21 &&\text{from \(n\).} \end{alignat*} Substituting, we obtain \(13y+10=21\) and so \[ y=\dfrac{11}{13}, \qquad x=\dfrac{29}{13}. \] The point of intersection is \(\Bigl(\dfrac{29}{13},\dfrac{11}{13}\Bigr)\).
  2. The lines \(l\) and \(n\) have the same gradient \(\dfrac{6}{5}\). The line \(l\) has \(x\)-intercept \(\dfrac{7}{6}\), and the line \(n\) has \(x\)-intercept \(\dfrac{13}{12}\). So \(l\) is parallel to \(n\), but \(l\ne n\).
  3. The gradient of \(l\) is \(\dfrac{2}{3}\) and the gradient of \(n\) is \(\dfrac{4}{5}\). So \(l\) meets \(n\), but \(l\) is not perpendicular to \(n\).

    We have
    \begin{alignat*}{2} 15y &= 10x-5 &\qquad&\text{from \(l\),}\\ 12x &= 15y-21 &&\text{from \(n\).} \end{alignat*} Substituting, we obtain \(12x=10x-5-21\). So \(x=-13\) and \(y=-9\). The point of intersection is \((-13,-9)\).
  4. Rearranging \(15y-6x-6=0\) gives \(5y=2x+2\). So \(l\) and \(n\) are the same line.

Exercise 8

Consider the line \(l\) with equation \(ax+by+c=0\) and the point \(P(x_1,y_1)\).

  1. Show that the line through \(P\) parallel to \(l\) is given by \(ax+by=ax_1+by_1\).
  2. Show that the line through \(P\) perpendicular to \(l\) is given by \(bx-ay=bx_1-ay_1\).

Next page - Content - Perpendicular distances